Revised 8 June 2023
Accepted 8 August 2023
Available Online 12 September 2023
- DOI
- https://doi.org/10.55060/j.gandf.230912.001
- Keywords
- Diatoms
Genetics
Photonics in nature
Gielis superformula - Abstract
The link between shape and function allows understanding the evolutionary success of several organisms and their constituent parts. This is true in particular for diatoms, unicellular microalgae which contribute massively to primary production and carbon sequestration on a global scale, and which are characterized by an impressive diversity in dimension and shape within about 103 genera and up to 105 estimated species. The peculiar feature of diatoms is the frustule, a porous silica shell which encloses the protoplasm and which is characterized by the presence of regular patterns of micro- and nano-pores in an ultra-structured architecture. The diatom frustule seems to be involved in mechanical protection of the cell, sorting of nutrients from noxious agents, gas exchange, and efficient coupling with solar radiation. The aim of this short review is to give on one hand an overview of the main genetic mechanisms which finely control frustule morphogenesis and, on the other hand, to focus on its photonic properties, which could contribute to understand the extraordinary efficiency of diatoms in photosynthesis. The discussion on frustule morphogenesis and optical functions has been linked to Gielis transformations as an elegant and efficient tool to describe its geometry.
- Copyright
- © 2023 The Authors. Published by Athena International Publishing B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (https://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Every five breaths we take, one is due to diatoms [1]. Diatoms are indeed the major and most diverse group of phytoplankton, contributing massively to global primary production (up to ∼20–25% [2]) and being responsible of about 240 Tmol of annual biogenic silica precipitation [3]. They are ubiquitous, single-celled algae whose protoplasm is in fact enclosed in a silica micro- and nano-patterned cell wall, called frustule [4]. Frustules consist of an epitheca overlapping a hypotheca in a “petri-dish-like” arrangement. Every theca is formed by a valve and a series of lateral bands (girdle bands) connected along the margins. The full series of girdle bands form the so called cingulum. Valves and girdles are provided with periodic or quasi-periodic distributions of pores whose dimension ranges between some tens of nanometers up to about one micron, depending on the species and on the specific location within the frustule [5]. It is hypothesized that the main functions of the frustule include mechanical stability improvement [6], sorting of nutrients from harmful agents [7], and optimization of sunlight harvesting [8]. Diatoms colonized, through tens of millions of years, all seas and freshwaters on Earth. About 103 genera and 105 species of diatoms are estimated, every species being characterized by its own frustule with specific dimension, shape, and symmetry (see frustule details for three different species in Fig. 1). The identification of the radial or bilateral symmetries of the frustule leads to non-phylogenetic classification of diatoms into centric or pennate types, respectively [5].

Scanning Electron Microscope (SEM) images of frustule details for different diatom species. (a-b): Coscinodiscus wailesii ; (c-d): Arachnoidiscus ehrenbergii ; (e-f): Stephanopyxis turris. Scale bars: 50 μm (a); 10 μm (b); 50 μm (c); 20 μm (d); 1 μm (e); 500 nm (f). Credit: Dr. Principia Dardano (see Acknowledgments).
The process of frustule formation is under the control of a finely tuned, species specific genetic mechanism which is still not fully explained in all its aspects [9]. After sequestration of monosilicic acid (Si(OH)4) dissolved in water, biosilica is synthesized within a membrane-bound cellular structure known as silica deposition vesicle (SDV).
Several organic molecules and proteins including long chain polyamines (LCPAs), silaffins and silacidins are implicated in silica patterning [4]. However, how the highly ordered frustule is formed and what are the exact spatial and temporal steps imparted during the morphogenesis process (including phase separation and reaction-diffusion of the involved biomolecules; polymerization, deposition, and spatial distribution of silica; SDV expansion and growth) is still under investigation [10].
The periodicity of the ultrastructure and the astonishing similitude with artificial photonic crystals [11] led to deepen, in particular, the optical properties of the frustule [11,12], which include the ability to couple light in guided modes [13], to collect and focus photosynthetic active radiation (PAR, λ = 400–700 nm) [14], to support photonic pseudo-band gaps [15], and to screen the cell from detrimental ultraviolet radiation (UVR) [16,17,18]. The ability of diatoms to manipulate light in more or less complex ways could explain their extraordinary photosynthetic efficiency.
The peculiar physical properties of bare or modified frustules have been exploited in several fields, e.g. in optoelectronics [19], catalysis [20], biochemical sensing and biosensing [21,22], solar energy harvesting [23], biomedicine and drug delivery [24], to name a few, and new innovative applications are repeatedly envisaged [10].
In present work we reported on the genes and macromolecules putatively involved in frustule morphogenesis; secondly, examples of light manipulation by diatom frustules have been mentioned and related to their shape and simmetry; finally, the possibility to make use of Gielis transformations in order to describe the diverse frustule geometries and ultrastructure is introduced [25].
2. FRUSTULE MORPHOGENESIS: THE MOLECULAR MACHINERY
Most of the available information on genes and molecules involved in frustule morphogenesis comes from studies on few species. In particular, Phaeodactylum tricornutum and Thalassiosira pseudonana are the two molecular model species, since P. tricornutum is characterized by a cell wall poor in silica [26], while the centric T. pseudonana has been developed as a model species to study the formation of diatom biosilica [27]. More recently, Cylindrotheca fusiformis has been exploited as well as model for studies on the silicification process [28].
The most characterized genes involved in frustule biomineralization encode the silicic acid transporters (SITs), which transport silicic acid from water into the cell [29]. Si-transporter genes are constituted by several members with differences in SITs family size and functionality, that play different roles in the uptake of silicic acid with different cellular localizations, Si binding affinities, and transport rates. From an evolutionary point of view, the SITs genes display sequence homology with proteins present in bacteria, most likely acquired by diatoms through horizontal gene transfer [30]. Analysis of knockdown mutants of the two SITs in T. pseudonana suggests for these transporters also a role in the sensing of cellular silicic acid levels, independently of the transport, controlling cell wall formation and cellular division process [31].
The first protein isolated from the cell wall of a diatom was the so called frustulin [32]. Frustulines are present across the cell wall, suggesting a specific function in frustule protection [33], but do not play an active role in biosilica formation. On the other side silaffins, silacidins, pleuralins and cingulins are proteins strictly confined to the SDV membrane, the silicalemma, and are able to promote polymerization and deposition of silica from inorganic precursors [34]. Silaffins are able to precipitate silica in vitro, forming spheres or plates containing regularly distributed nano and micro pores [35]. The primary structure of a precursor of silaffins was isolated for the first time in C. fusiformis [36], and later other genes have been found in different diatom species. All the silaffins identified so far are subjected to different post-translational modifications during intracellular maturation, which are necessary for the formation of silicon dioxide [33]. Like silaffins, also silacidins are phosphorylated and the high degree of phosphorylation of the serine residues is related to their ability to precipitate silica nanospheres [37]. Pleuralins are associated to the pleural bands, the regions of overlap between the two thecae of the frustule. Pleuralines are not encoded in all the genomes sequenced so far. In the case of C. fusiformis it is hypothesized that they are able to bind simultaneously silaffins and frustulins, in order to connect epitheca and hypotecha at the girdle bands [38]. Unlike sillaffins and silacidins (mainly involved in silica precipitation and deposition), cingulines seem to be crucial in the molecular mechanisms of silica assembly [34], being in particular involved in the morphogenesis of the cingulum (as their name suggests).
The main organic and soluble fraction of the biosilica matrix in diatoms is given by long-chain polyamines (LCPAs) [39]. Like silaffins and silacidins, they are able to precipitate silica in vitro. They display species-specific differences in degree of methylation, chain length and position of secondary and tertiary amines [40], suggesting that they may be directly responsible for the morphological differences in the frustules of different diatom species [34]. Furthermore, it has been hypothesized that LCPAs control the expansion process of the SDV by interacting with its lipidic membrane during cingulum and thecae formation [40].
The overall frustule morphogenesis process seems to be based on phase separation of proteins and LCPAs which in turn forms a scaffold on which silica precipitates inside the SDV [41]. This may be an iterative process in which larger droplets of biomolecules form, around which silica deposits. The holes in the silica matrix in turn form domains in which smaller droplets of biomolecules form, around which silica again precipitates. However, the components involved in the biogenesis and scaffold of the frustule are very complex and current knowledge is not exhaustive in order to explain the frustule shape evolution in different species of diatoms. In the near future, the integrative sequence analysis of the genomes of other diatom species will be available thanks to the “100 Diatom Genomes Project”, that will allow sequencing 100 diatom species from across the tree of life [42]. This will help to shed light on the key genes that mediate differences in cell wall shape symmetry and size between distinct species. In addition, it should be noticed that, while genetics are the main factors in determining diatom frustule shape, environmental factors have an important effect as well.
3. DIATOM FRUSTULES AND LIGHT MANIPULATION
Since the appearance of life on Earth, Nature has provided numerous organisms, including algae, plants, and animals with structures at the sub-micron scale able to finely manipulate light, e.g. for intra-species communication, inter-species interaction, camouflage or to enhance photosynthetic efficiency. These structures can work as 1D, 2D or 3D photonic crystals; as polarization-selective reflectors, diffraction gratings, or give rise to disordered systems able to produce high levels of transparency, whiteness or blackness [43]. Among all, the organisms who deserved the explicit classification of “living photonic crystals” have been diatoms [13]. Photonic crystals (PhCs) are characterized by a periodic distribution of refractive index arranged and dimensioned in a way to couple light at specific wavelengths and directions of propagation and/or to inhibit the transmission of light whose wavelength lies in a specific spectral range [44]. In analogy with the energy band gaps present in semiconductors, these forbidden spectral ranges are known as photonic band gaps (PBGs). If locally modified, PhCs can guide or confine light, giving rise to PhC waveguides and nanocavities, respectively.
In 2004 Fuhrmann and coauthors were the first to numerically retrieve the photonic band structure of a diatom frustule looking at valves and girdles of Coscinodiscus granii as photonic crystal slabs, also evaluating the efficient optical coupling of the chloroplasts with the evanescent waves associated to the modes guided by the frustule [13]. More than 15 years later, Goessling et al. experimentally detected by means of micro-scatterometry the presence of a pseudo-bandgap (i.e. a PBG that only exists for specific directions of propagation) associated to the girdle of the same species, both in air and in water. Also waveguiding of green radiation has been experimentally observed [15]. Very recently, the spatial mapping of modes guided by Nitzschia filiformis valves has been experimentally accomplished by means of scanning near-field optical microscopy (SNOM), while finite difference time domain (FDTD) numerical simulations allowed evaluating how the amount of spatial disorder in pore location is able to enhance light coupling efficiency [11].
The valves of several species of centric and pennate diatoms are able to collect and confine optical radiation in more or less complex patterns, acting as microlenses (see Fig. 2). It has been shown that Coscinodiscus wailesii valve is able to focus coherent radiation at λ = 785 nm in a 10 μm wide spot at a distance of about 100 μm away from the valve itself. The phenomenon is ascribable to the coherent superposition, along the propagation axis, of the diffraction contributions coming from the single pores of the valve and it has been observed also for incoherent visible radiation, for the same species [14] and for Arachnoidiscus ehrenbergii [45], Coscinodiscus centralis [46], and Ctenophora pulchella [18] species. The position of the light spots along the optical axis depends on the wavelength of the incoming radiation. Indeed the divergence angle of the light diffracted by a single pore is proportional to wavelength, thus, the longer the wavelength, the closer to the valve the focused spots take place. For sufficiently short wavelengths, the light confinement occurs quite far from the valve or does not take place at all [14,17 ,18,45]. This is one of the mechanisms by which diatoms are able to efficiently collect photosynthetic active radiation and, simultaneously, protect themselves from detrimental ultraviolet (i.e. short-wavelength) radiation. Other mechanisms involved in UV-shielding are absorption by frustule silica and UV-visible wavelength conversion induced by nanostructured silica photoluminescence [8,17,18].
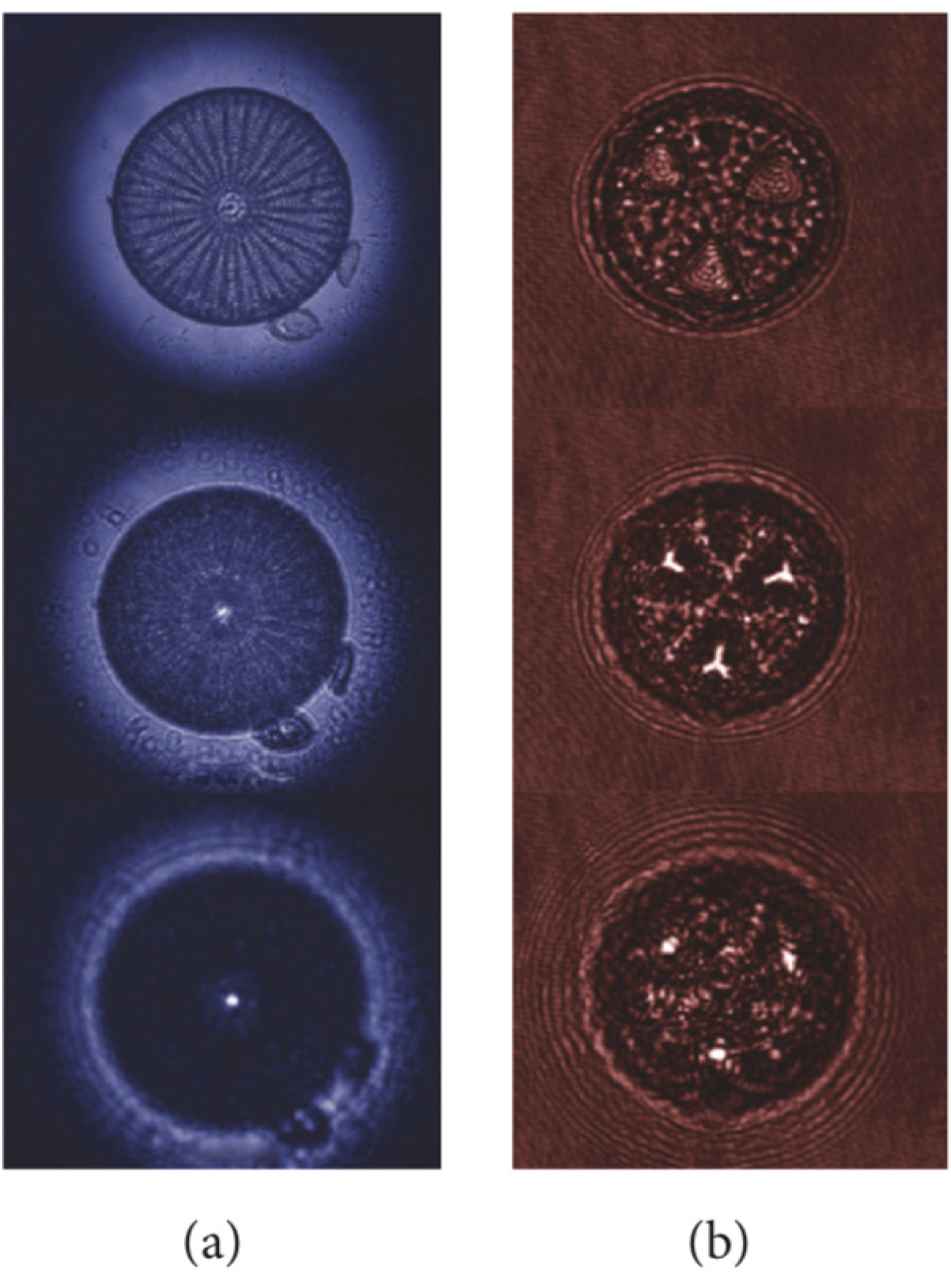
Transmission images (a) and intensity maps retrieved by digital holography (b) at different distances along the propagation axis for a single valve of Arachnoidiscus ehrenbergii and Actinoptychus senarius diatoms, respectively, showing light confinement in intense hot-spots. Reproduced with permission from [8].
We can conclude that diatom frustule photonic properties (including light coupling, waveguiding, scattering, diffraction, focusing, and spectral filtering) are likely involved in PAR harvesting mechanisms by contributing to its capture, redistribution, and retention, while attenuating or rejecting UVR, which is intrinsically detrimental for DNA (especially through formation of dimeric photoproducts between adjacent pyrimidines [47]).
4. GIELIS SUPERFORMULA AS A NEW TOOL FOR GENERATING FRUSTULE GEOMETRIC MODELS
When computing the photonic properties of diatom shells, it is fundamental to obtain accurate, 3D models of the frustule through which numerically simulate the propagation of the optical field [48]. Several algorithms are available to reconstruct the photonic band structure of the frustule, the presence of resonant or guided modes, the field transmitted by a valve and other optical features, and they include, among others, Finite Element Method (FEM), Plane Wave Expansion (PWE), Finite Difference Time Domain (FDTD) Method, and Wide-angle Beam Propagation Method (WA-BPM) [49]. In most cases, very simplified models are used in which frustule valves and girdles are approximated by silica slabs provided with periodic pore patterns characterized by precise values of diameters and lattice constants, which are quite far from the actual structures we can find in nature [13,15,50]. An alternative is represented by the possibility to retrieve a bidimensional refractive index map from a frontal-SEM image of a single valve, then extruding it in order to obtain a three-dimensional CAD model of the valve itself [14,17,18,45]. Even though this method allows reproducing the shell irregularities in the plane defined by the valve (e.g. the deviation from perfect periodicity of the pore pattern), the information on curvature is totally lost. Very recently, Ghobara et al. [12] applied frequency domain FEM to study near-field light modulation by Gomophonema parvulum frustule after reducing its complex 3D structure into 2D, statistically representative cross-sections and further disassembling their distinct optical components. The overall optical response of the frustule results from the overlay of the different optical phenomena associated to the integrated components.
An elegant way to describe complex geometries in an analytical closed form is given by Gielis superformula [51,52,53], which, in its 2-dimensional expression, represents a generalization of the circle equation:
The exponents n1,2,3 describe the basic polygons defined by the symmetry parameter m. When n1 = n2 = n3 = 2, f(ϑ) = R = 1, and A = B, Eq. (1) describes the unit circle, while, when A and B differ, the basic shape is an ellipse. Bi-dimensional superformula allows describing diatom valves of different shapes and symmetries by simply changing the value of the parameter m, since it divides the plane into m sectors. In particular, for m = 0,1,2,3,4, radially symmetric valves, 360° sectorized valves (not necessarily symmetrical), pennate valves, triangular, and square valves are respectively generated. For higher values of m, higher-order sectorized valves (e.g. the ones of Arachnoidiscus genus) can be described. When passing to three-dimensional superformula, also curvatures of the frustule surfaces can be taken into account:
This equation allows describing the frustule as a whole, the three-dimensional coordinate planes corresponding to the valvar, radial/transapical and the (per)apical planes. Furthermore, the arrangement of the pores within the frustule can provide a very specific coordinate system adapted to its shape. This geometrical approach provides a global representation of diatom frustules which, in combination with existing CAD and Finite Element studies, can potentially lead to study light propagation through valves and girdles more efficiently and at a higher level of accuracy.
5. CONCLUSION
A multidisciplinary approach, spanning from genetics to photonics and geometry, can represent an effective instrument in the understanding of the complex relationships which link frustule morphogenesis, shape, and its optical properties. Species-specific shapes, dimensions and pore patterns indicate a strict genetic control on frustule morphogenesis and functional analyses of the related proteins are necessary. Frustule shape, together with refractive index contrast respect to the surrounding environment, dictates the ways in which it manipulates optical radiation, enhancing light harvesting and, consequently, photosynthesis. New geometrical tools based on Gielis transformations will allow computing the propagation of optical fields through the intricate but regular diatom shell ultrastructure in a global and easier way if compared to traditional methodologies.
Acknowledgments
The authors thank Dr. Principia Dardano from the Institute of Applied Sciences and Intelligent Systems of the National Research Council, Unit of Naples, for allowing the use of the SEM images reported in Fig. 1.
Conflict of Interest
The authors declare no conflicts of interest.
Data Availability
This is a review article. No original data have been produced for this study.
Funding
The authors declare that no funding was used for this study.
Authors’ Contribution
Edoardo De Tommasi and Alessandra Rogato contributed equally to the manuscript.
REFERENCES
Cite This Article

TY - JOUR AU - Edoardo De Tommasi AU - Alessandra Rogato PY - 2023 DA - 2023/09/12 TI - The Diatom Frustule: Morphogenesis and Role in Light Manipulation JO - Growth and Form SP - 3 EP - 10 VL - 4 IS - 1-2 SN - 2589-8426 UR - https://doi.org/10.55060/j.gandf.230912.001 DO - https://doi.org/10.55060/j.gandf.230912.001 ID - DeTommasi 2023 ER -









