Revised 31 July 2023
Accepted 23 October 2023
Available Online 29 November 2023
- DOI
- https://doi.org/10.55060/s.atmps.231115.002
- Keywords
- Anisotropics
Mean curvature
Axially symmetric
Wulff shape
Crystallography - Abstract
In this article we discuss the construction of equilibrium surfaces with symmetry for anisotropic energy functionals.
- Copyright
- © 2023 The Authors. Published by Athena International Publishing B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (https://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Anyone who has cut meat or sawed wood is aware that it is easier to cut or saw in some directions than in others. If we consider meat or wood as an idealized horizontal three-dimensional slab, then we observe that the amount of energy required to create a unit area of surface, depends entirely on the direction of the piece of surface.
The same phenomena is encountered when cutting through any crystalline solid, or more generally, through any material in an ordered phase. Since intermolecular bonds are stronger in certain directions than in others, more work must be done to cut along these directions and thus to create a unit area of surface along them. To account for this Josiah Gibbs introduced a notion of anisotropic surface energy by defining a density
The deviation of
According to the principles of thermodynamics, the tendency of a surface to minimize its surface energy is the most important factor in determining the surface geometry. Of course, this minimization must take into account any constraints which are imposed, for example boundary conditions, volume constraints. This tendency of the surface to minimize energy yields a differential equation, known as the Euler-Lagrange equation, which gives a necessary condition which any equilibrium surface must satisfy. The first one to apply the calculus of variations in relation to anisotropic surface energy was Pierre Curie [1].
At small scales, the shape of biological organisms is driven by their surface energy and not their bulk energy. In his epic work “On Growth and Form” [2], D'Arcy Thompson makes the case that biological organisms are, first and foremost, physical entities and therefore their morphology is, at least, partially driven by the laws of physics. He also makes the claim that the anisotropic nature of the constituent materials of these organisms is responsible for the deviation of their shapes from being spherical in shape.
Although he does not explicitly use an energy of the form in Eq. (1), he employs the anisotropic Young-Laplace equation:
Remarkably, the type of energy defined in Eq. (1) possesses a canonical equilibrium known as the Wulff shape. We can consider the density γ as a function defined on the unit two-dimensional sphere S2 in three-dimensional space. As each point ν ∈ S2, we consider the half-space {X ∈ R3 | X · ν ≤ γ(ν)}. The intersection of all such half-spaces defines a convex body whose boundary W is called the Wulff shape, i.e.:
A series of results, collectively known collectively as Wulff’s Theorem, state that the surface W is the unique absolute minimizer of the free energy (Eq. (3)) among all closed surfaces enclosing the same volume as W [3,4] (for other values of the volume, the minimizer is the appropriate rescaling of W). Some biographical information on Georg Wulff can be found in [5]. In the special case γ ≡ 1, Wulff’s Theorem is just the classical three-dimensional isoperimetric inequality which states that the round sphere is the unique minimizer of surface area for a given volume. The Ukrainian crystallographer Wulff first stated this result in the case where W and all competing surfaces are “crystals”, i.e. surfaces that are piecewise linear. Over the years, Wulff’s result has been generalized to the point where it is now known to hold (in any dimension) when W is an arbitrary convex surface and the comparison surfaces need only be surfaces in some measure theoretic sense.
Besides the result that the Wulff shape W is the unique minimizer, there are results characterizing W as the unique stable closed equilibrium surface, the unique embedded closed equilibrium and the unique genus zero, closed equilibrium for the surface energy (Eq. (3)).
2. DELAUNAY SURFACES
The axially symmetric constant mean curvature surfaces were found by Charles Delaunay [6]. Delaunay found that if a conic section is rolled without slipping along a line, the trace of a focus will yield the generating curve of a CMC surface and that all axially symmetric CMC surfaces arise in this way. The correspondence is as follows: circle ←→ cylinder, ellipse ←→ unduloid, hyperbola ←→ nodoid, parabola ←→ catenoid. The sphere can be obtained as a limiting case of unduloids. The integration of the equation for the rolling curve is reminiscent of another important appearance of the conic sections; Kepler’s integration of the equations of motion of an object subjected to a central force field. It is likely that Delaunay, who was an astronomer by profession and who had written his dissertation on variational calculus, was influenced by Kepler’s calculations.
Now consider an axially symmetric anisotropic surface energy functional F. This is equivalent to the Wulff shape W being axially symmetric and we let (u(v),v) denote the generating curve of W . Let µ1, (respectively µ2) denote the principal curvature of W along a meridian, (respectively a parallel), with respect to the inward pointing surface normal of W. Likewise, we let κi denote the corresponding principal curvatures of an axially symmetric surface Σ, with respect to the outward pointing surface normal. In this case, the equilibrium equation reduces to:
The axially symmetric surfaces with constant anisotropic mean curvature will be called anisotropic Delaunay surfaces [7]. These can be found as follows. Let (r,z) denote the generating curve of such a surface Σ. To each point on Σ, there is a unique point on W where the normals to Σ and W agree.
Then at these points, u and r are related by the quadratic equation (see Fig. 1):
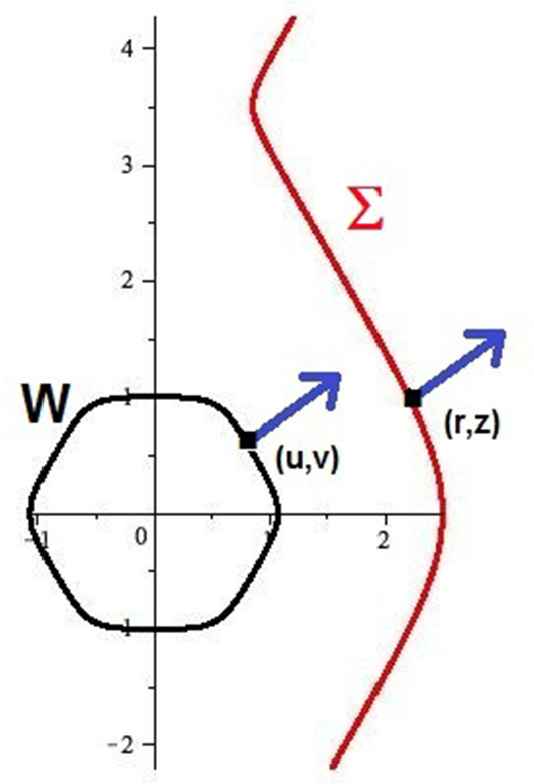
Generating curves of Σ and W.
To generate a wide variety of examples, we employ the Gielis formula [8]:
This formula is an excellent source of curves with prescribed symmetries yielding a curve in polar form. Its utility in modeling natural shapes in a wide variety of circumstances is reviewed in [9]. We refer to the polar graphs given by Eq. (5) as Gielis curves. Given two convex Gielis curves,
For this type of Wulff shape, the analogues of the constant anisotropic surfaces found above can be found by replacing the cross-sectional circles by the

Upper left: Wulff shape. Upper right: catenoid. Bottom left: unduloid. Bottom right: nodoid.
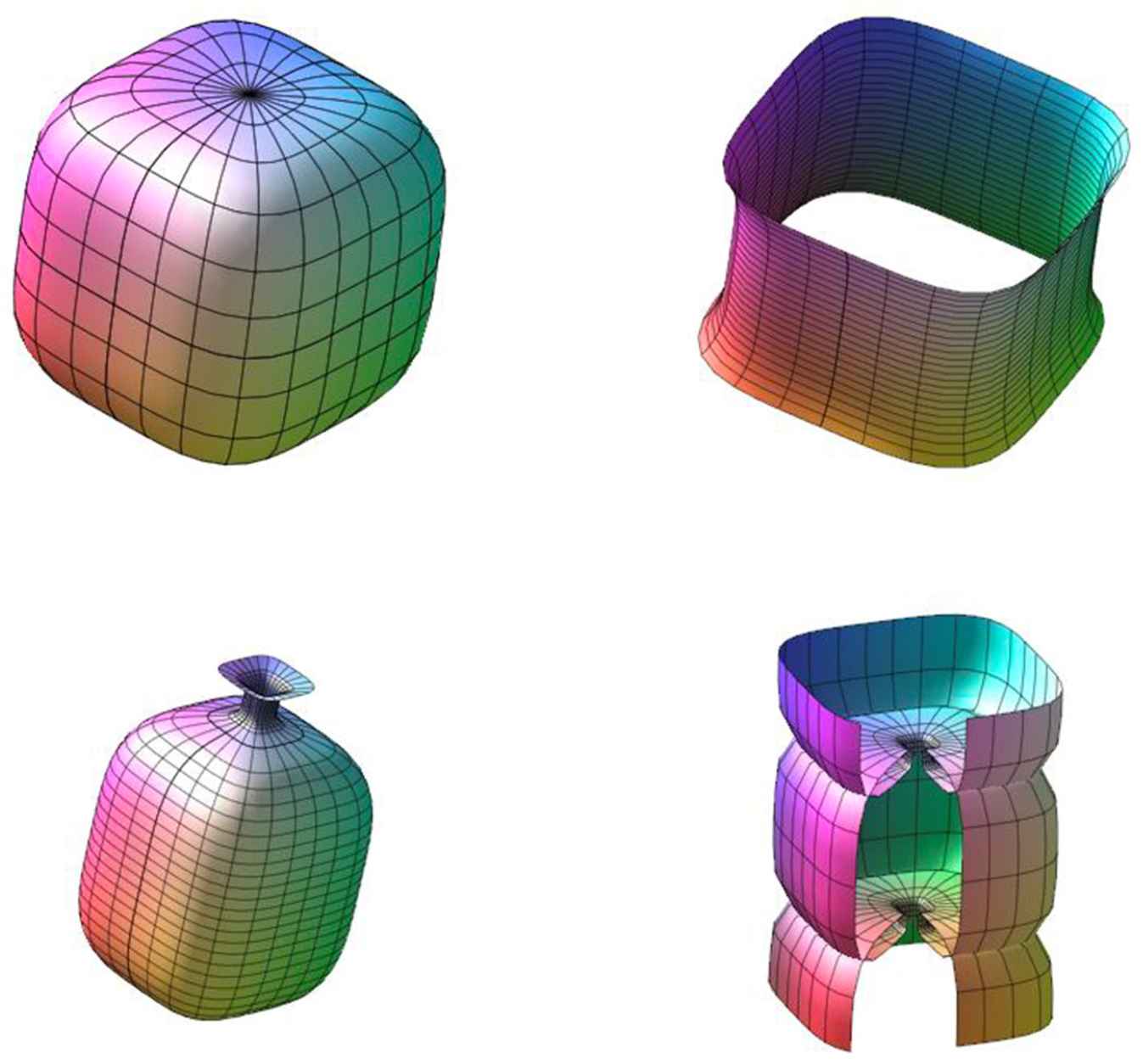
Upper left: Wulff shape. Upper right: catenoid. Bottom left: unduloid. Bottom right: nodoid.
There is at least one earlier appearance of a type of anisotropic Delaunay surface in the literature. Bernal and Fankuchen observed that equilibrium droplets of a type of nematic liquid crystal which was extracted from tobacco plant virus, take a form which they refer to as a tactoid, which resembles an American football. They state that the surface of these shapes satisfies Eq. (2).
3. HELICOIDAL SURFACES
Oscar Perdomo [11] gave a remarkable generalization of the rolling construction which produces constant mean curvature surfaces which are invariant under a helicoidal motion. Such surfaces are known as CMC twizzlers.
The immersion is represented as the orbit of a planar generating curve
Perdomo’s construction generalizes to the anisotropic cases provided that the Wulff shape W is smooth and axially symmetric [12] (see Fig. 4, Fig. 5 and Fig. 6). The only modification in the construction is that Eq. (8) is changed to:
It is worth noting that if a helicoidal or axially symmetric surface is represented in non-parametric form

Upper left: Wulff shape for
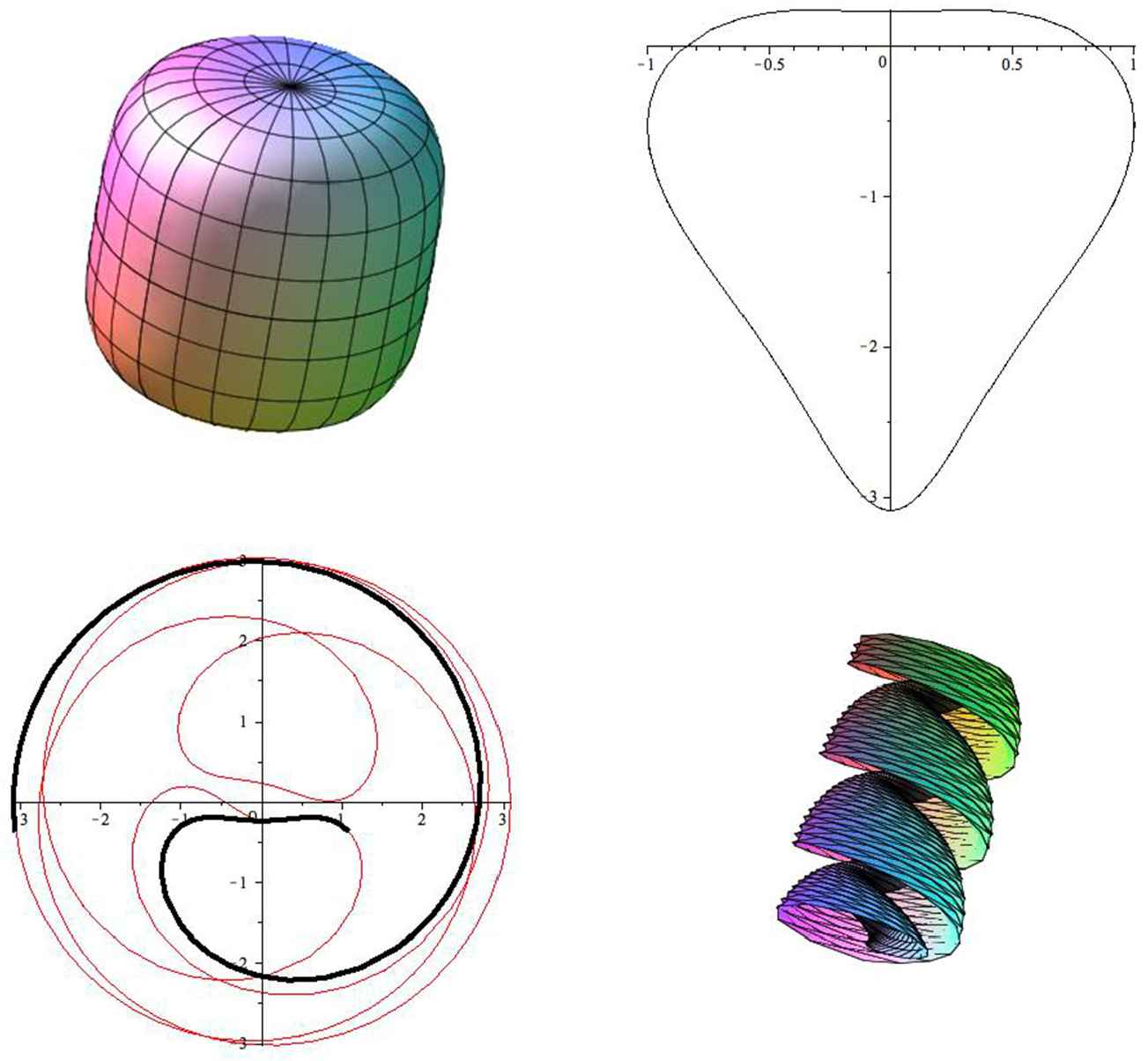
Upper left: Wulff shape for
Upper left: Wulff shape for
4. ROTATING ANISOTROPIC DROPS
We will consider the equilibrium shape of a non-liquid drop rotating with a constant angular velocity
The total energy is thus of the form:
In the special case
To see this, we note that the principal curvatures of
For closed genus zero surfaces we can let r approach 0 and we obtain that
The discriminant is
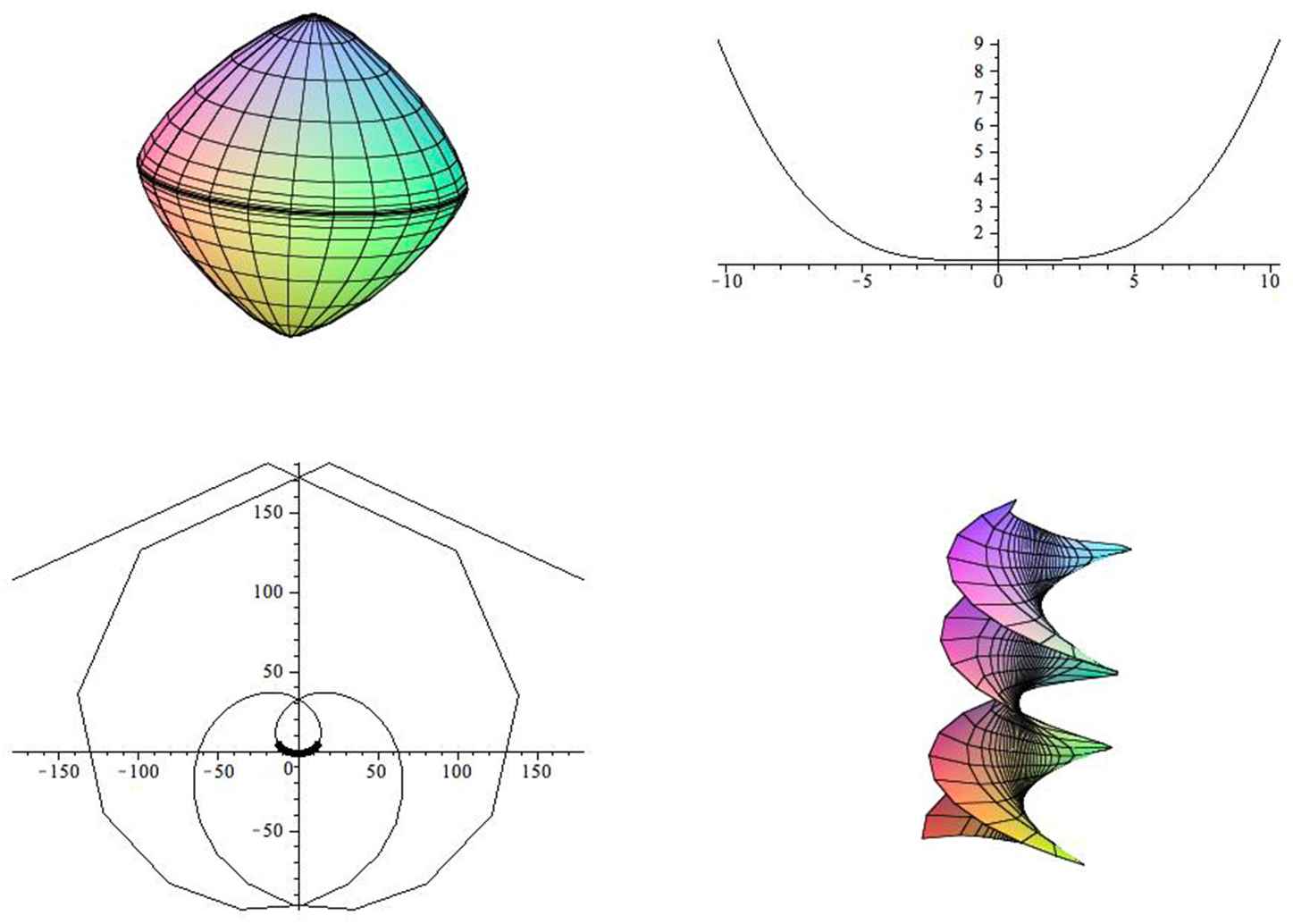
Surfaces of this type are shown in Fig. 7 and Fig. 8.
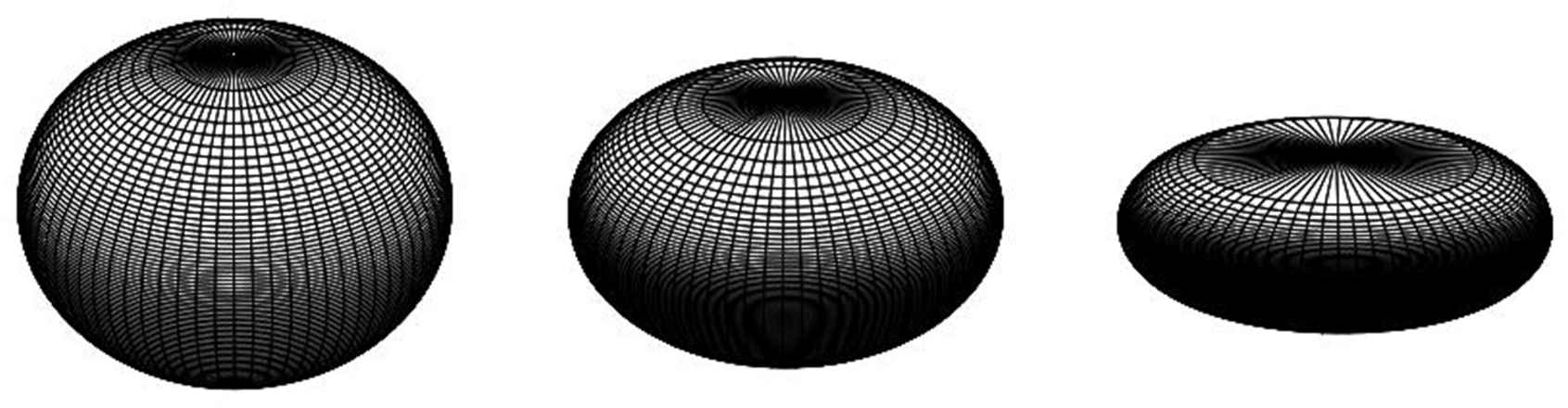
Equilibrium drops for the functional
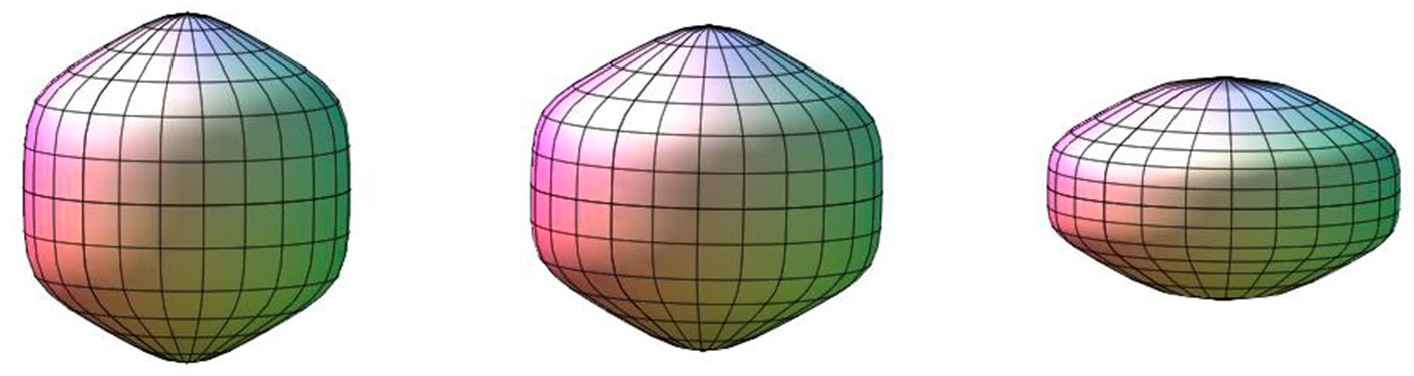
Equilibrium drops. Left:
We will describe a construction of the part of the generating curve
In this case,
For
For
For
In all three cases, the vertical coordinate of the generating curve
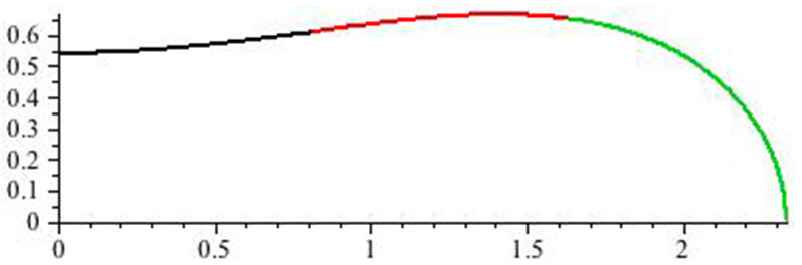
Gluing branches of the profile curve.
REFERENCES
Cite This Article

TY - CONF AU - Bennett Palmer PY - 2023 DA - 2023/11/29 TI - Construction of Equilibria With Symmetry for Anisotropic Energy Functionals BT - Proceedings of the 1st International Symposium on Square Bamboos and the Geometree (ISSBG 2022) PB - Athena Publishing SP - 21 EP - 29 SN - 2949-9429 UR - https://doi.org/10.55060/s.atmps.231115.002 DO - https://doi.org/10.55060/s.atmps.231115.002 ID - Palmer2023 ER -









