Revised 6 August 2023
Accepted 19 October 2023
Available Online 29 November 2023
- DOI
- https://doi.org/10.55060/s.atmps.231115.011
- Keywords
- Superellipses
Superformula
Optimization
Technological applications - Abstract
In 1997, the Superformula was developed as a generalization of superellipses and supercircles. An overview is given of the various developments that led to this generalization and its extensions to 3D. From the earliest steps onwards, optimization in nature and technology has been a driving force.
- Copyright
- © 2023 The Authors. Published by Athena International Publishing B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (https://creativecommons.org/licenses/by-nc/4.0/).
1. SUPERCIRCLES AND SUPERELLIPSES
1.1. Supercircles and Their Pi’s
ChatGPT provides the following response when asked to provide information on the superformula: “The Superformula is a mathematical formula first introduced by Johan Gielis in 2003. It is a generalization of the traditional mathematical formula for simple shapes such as circles and ellipses and can be used to describe a much wider range of shapes, including shapes that are complex and organic in nature. The superformula has been applied in a number of fields, including computer graphics, biology and physics, and is known for its versatility and simplicity. It has been called “the most beautiful formula” by some mathematicians and scientists”. Following the original publication [1,2] the Superformula has been applied in many fields [3]. The focus of this contribution is on applications in technology. Some may even have the potential to change entire industries. The “Superformula” as we know it today, actually saw the day of light in the summer of 1997. It is a generalization of the Cartesian equation describing supercircles and superellipses.
Superellipses and supercircles are a subset of so-called Lamé curves. Gabriel Lamé (1795–1870) was the first to generalize the Cartesian equation of ellipses [4]:
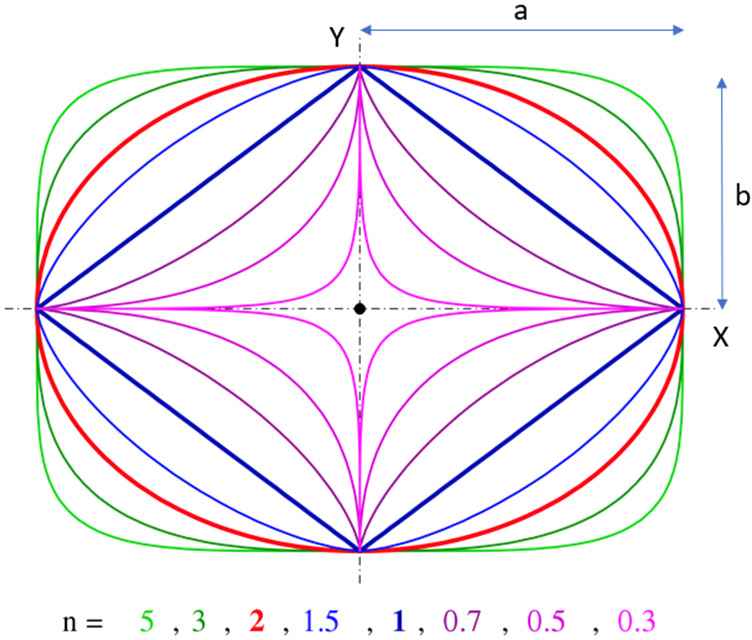
A set of basic superellipses.
To determine area, all calculations on these curves were done with Cartesian coordinates [8,9]. In practice, this caused computational problems, especially at the points where the curve intersects the X-axis. When using Cartesian coordinates, the slope for the superellipse is infinite as x approaches a.
In 1997, it could be shown that computations would be easier and more effective if polar coordinates were used [10]. The distance from the pole is called the radial coordinate, radial distance or simply radius (r) and the angle is called the polar angle. The transition of the equation for superellipses from Cartesian to polar coordinates is straightforward:
This derivation is documented in the thesis “Supershapes, roots and bamboo” [10] and forms the first step towards the superformula. This methodology enabled stabler and faster numerical computational methodologies for perimeter, area and moments of inertia, in engineering applications.
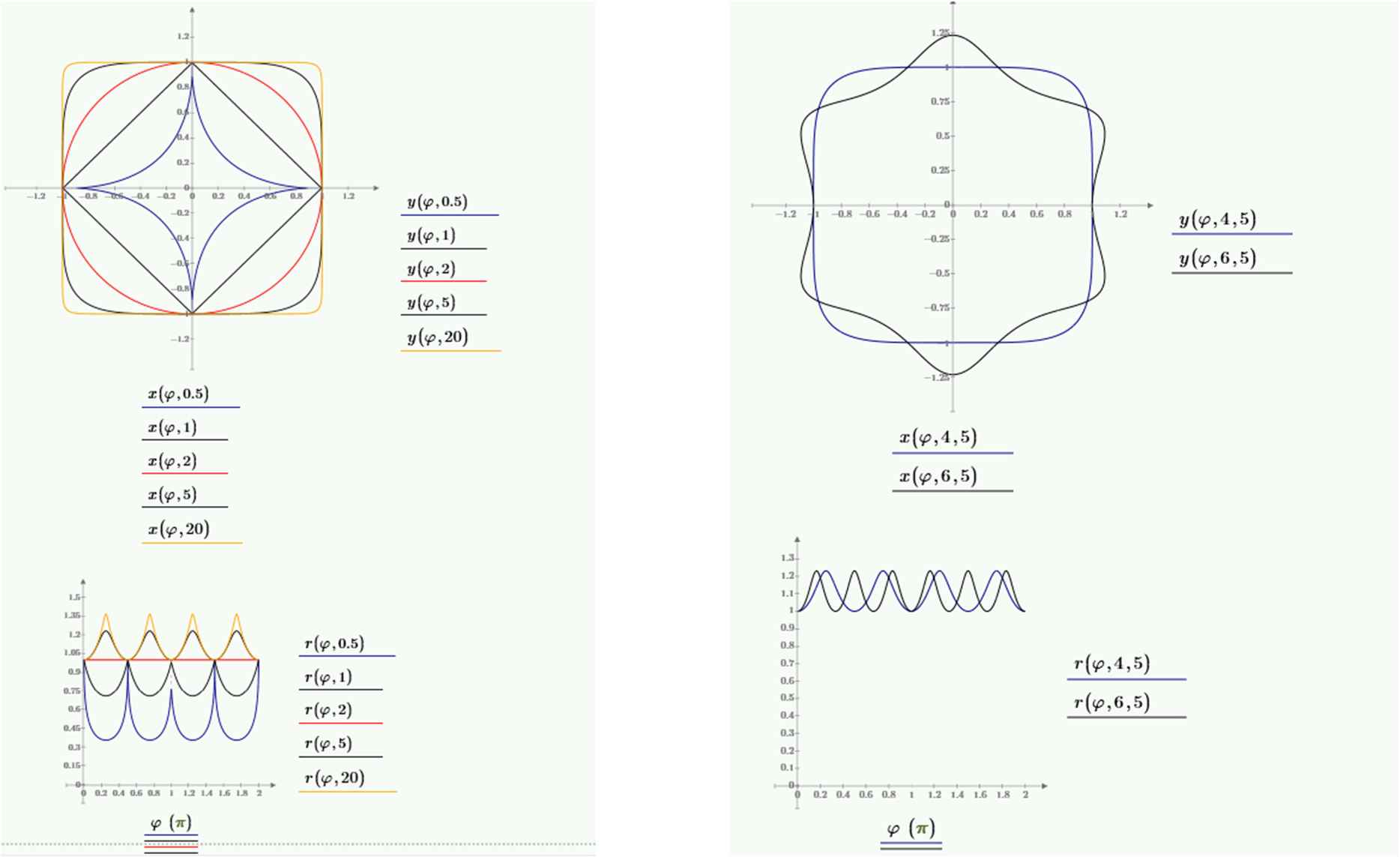
1.2. Pi Is a Function
For each of the shapes, specific trigonometric functions can be defined [10,11]. Fig. 2 shows cosines and sines for various values of n (0.5, 1, 2, 5 and 20). It later turned out that there was already a large body of literature on the subject [12,13] and these functions give rise to Pythagorean Theorems adapted to the shape [14]. With each shape, a very specific Pythagorean Theorem is associated [13,14]. Alternatively, Eq. (2) can be considered as a transformation of a circle but can also transform other functions. Fig. 3 shows the transformation of the classical tangent function via multiplication of the radial function.
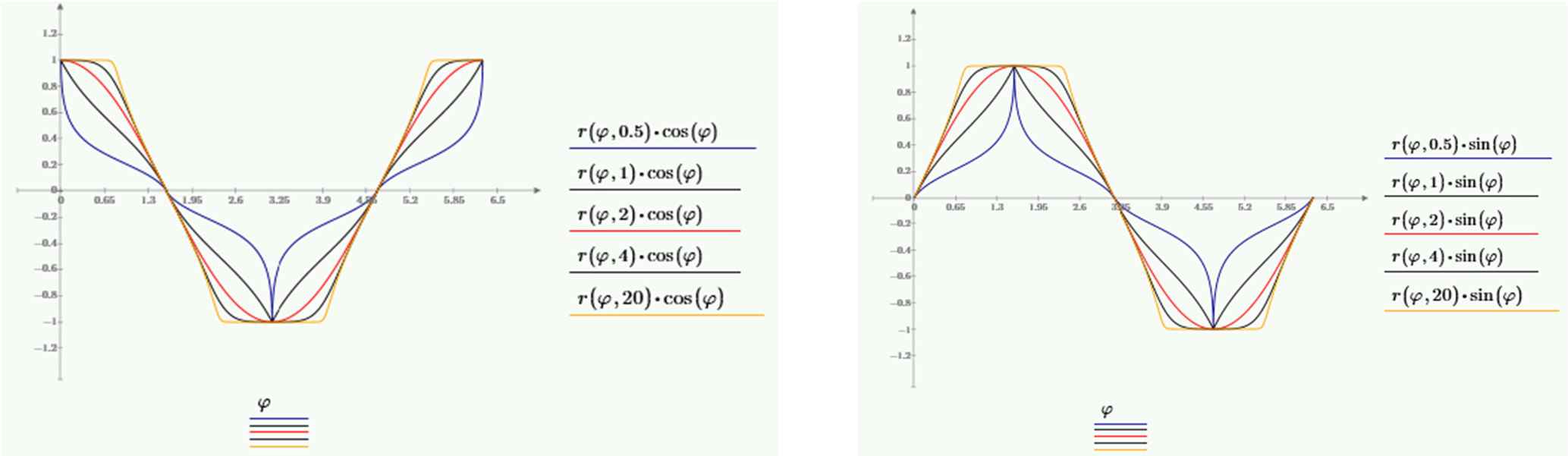
Cosines and sines on supercircles for
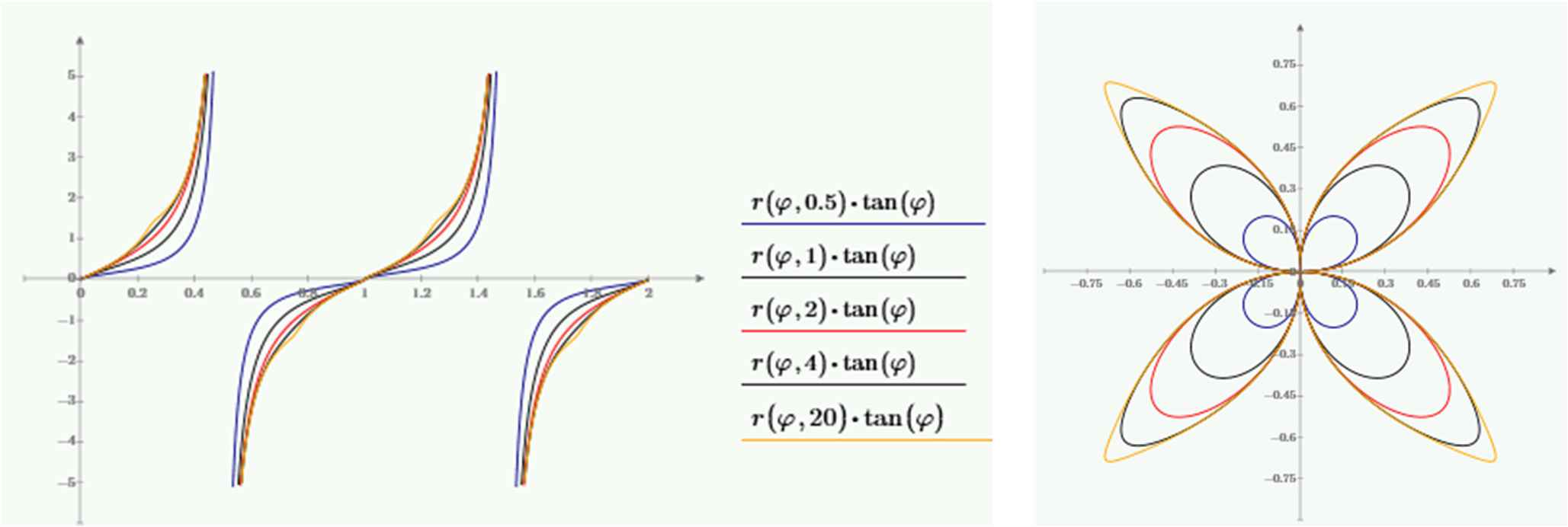
Left: tangent functions with operator. Right: cosine and sine in Eq. (2) are replaced by cotan and tan respectively. For both panels graphs are shown for
Pi is the ratio of the circumference of a circle to its diameter, or half the circumference to its radius. Using the idea of Gabriel Lamé, one possible generalization is to calculate the circumference of the Lamé-shape and divide it by the distance between the points at 0° and 180°. As the Lamé-shape has a combination of mirror- and point symmetries, we can calculate the length of the curve over 45° and multiply that value by 8 to get to the circumference of a full shape.
When defining the length of the halfperimeter of a supercircle as
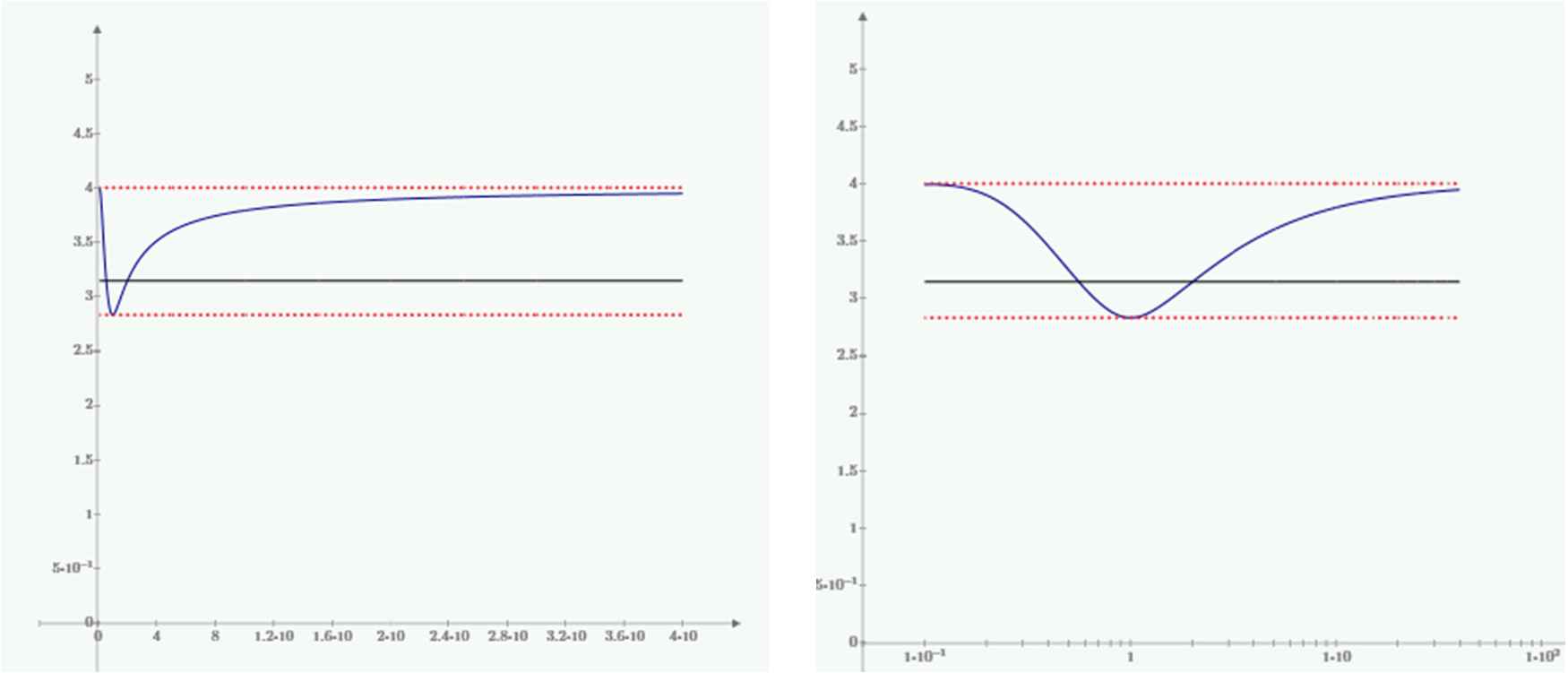
It can be seen that for any Lamé-shape the
It is also observed that there are two shapes that have the conventional value of
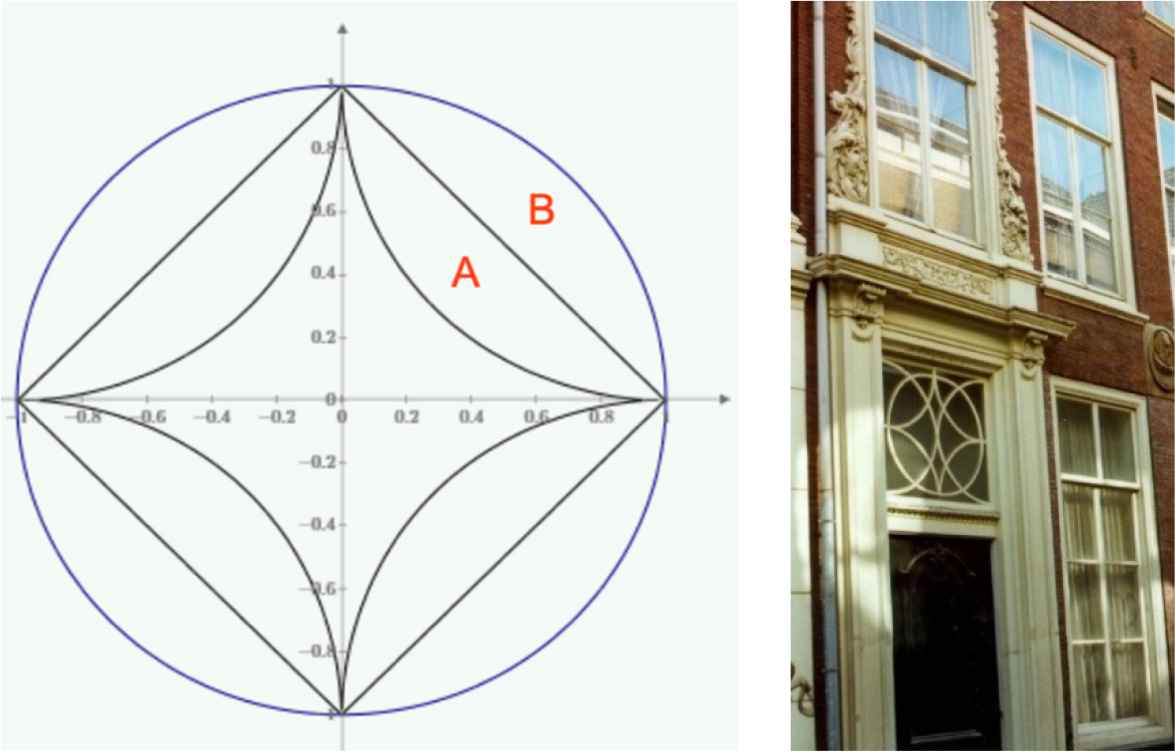
Left: supercircles with exponent 2, 0.561494 and 1. Right: front door of the house of Simon Stevin (1548-1620) in The Hague, Netherlands.
2. THE SUPERFORMULA
Despite their usefulness for modeling stems of quadratic bamboos and plants in general, a major drawback of superellipses and supercircles is their restriction to 4-symmetry, which means that all quadrants have essentially the same shape. In the summer of 1997, Johan Gielis was deep in thought about plants and the results obtained in [10] when he understood that the shapes would have different symmetry values if you changed the base frequency of the function
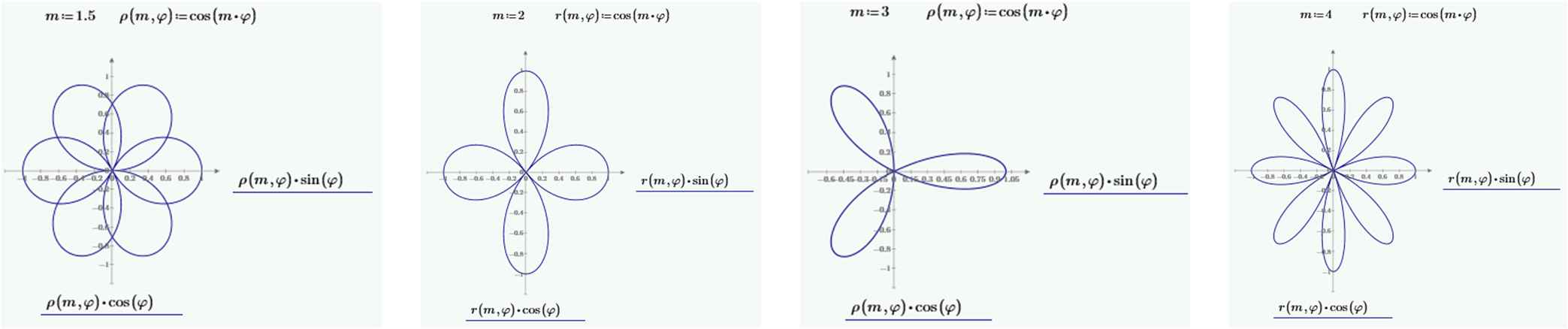
Rhodonea curves for integer and non-integer values of m. The left one is also shown in [15].
By using this insight, the superformula was born [1,2]. Below the various steps are described.
The symmetry parameter
Supercircles (left) and supershapes (right). Both the shapes and the values of
Other changes to the superformula included generalizations of exponents and the use of the superformula as a transformation on planar functions (Eq. (4), Fig. 8). Like in Rhodonea curves, m can be an integer, a rational or an irrational number.
The superformula can indeed be considered as a transformation on functions. If multiplied by a constant value, supercircles result, but
Introducing a rotation is achieved by introducing phase differences (Fig. 9 left) and different phases lead to shearing-like transformations (Fig. 9 center and Fig. 9 right). Also, the trigonometric functions can be different. In Fig. 2 the trigonometric functions cos and sin are replaced by cotan and tan:
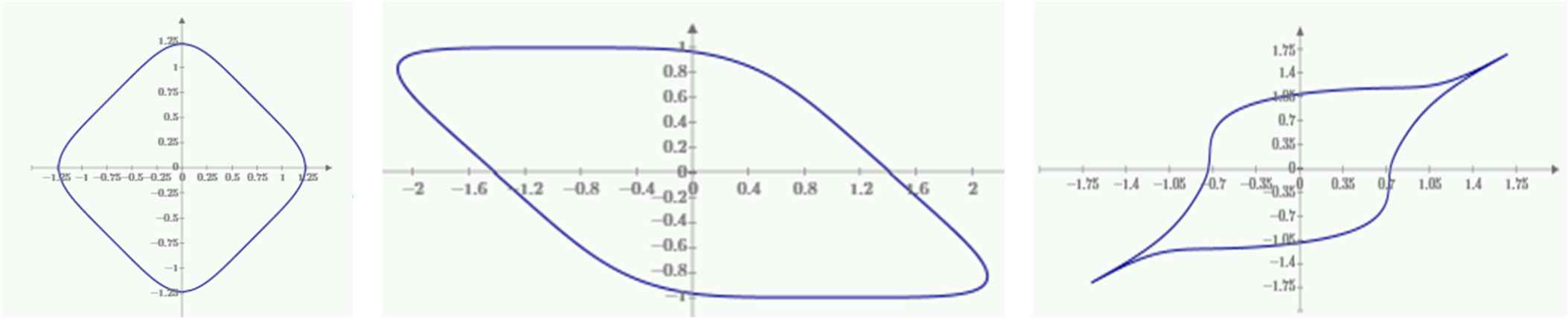
Difference between alfa and beta phase. Left:
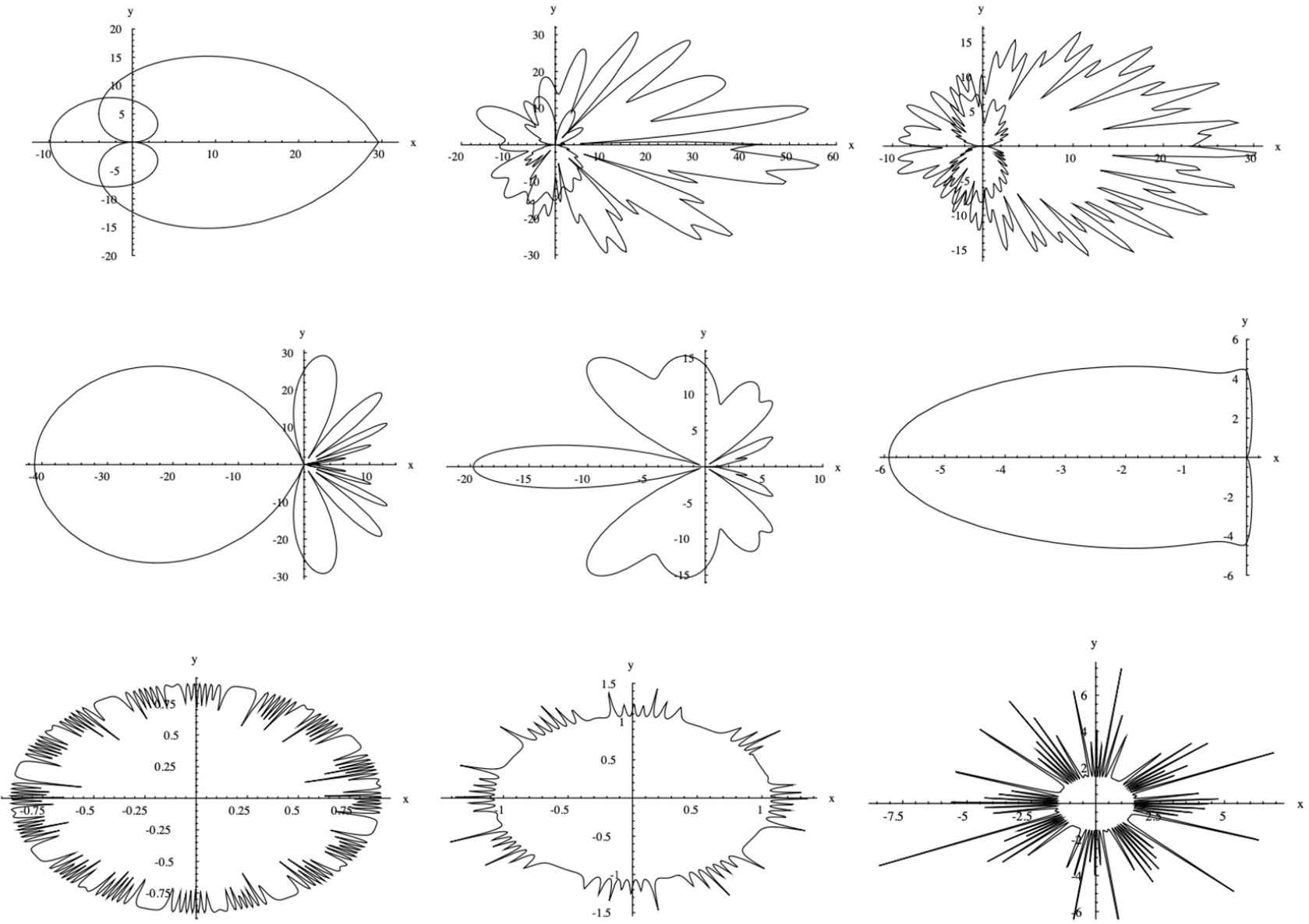
Examples of generalized Gielis transformations [20].
3. EXTENDING THE SHAPE PALETTE
3.1. Variations With C-Points
Initial developments focused on the graphics industry. Graphic artists and designers, confronted with the challenge of developing new designs and shapes in 2D and 3D, are constantly looking for new shapes and patterns. Based on the original Superformula, variational shapes can be introduced in a variety of software products.
For Adobe Illustrator and Photoshop a plug-in was developed for users to experiment with 2D shapes, but also with combinations of these shapes. Supergraphx products and applications provide such solutions for graphic arts in 2D, 3D and animation. Supergraphx transforms the PC from being a computing tool into an extension of human imagination and creativity, capable of generating anything one can think of. In this graphical user interface parameter
This added important new features for graphic artists in 2D, giving them access to a vast number of new shapes. The controllability of the shapes does not allow full control, since these features are already present in the vector-based drawing software of Illustrator and Photoshop. While providing the user with a diversity of forms (Fig. 11, Fig. 12) generated in real time, the program also allows the user to change and control the results, either using the C-points or through native Illustrator technology. In addition, the interface also allows for variation. When ‘variation’ is clicked, the user will see a collection of nine shapes that differ more or less from the initial shape, in one or more of the parameters of the formula, including C-points. When clicking on one of these shapes, nine other shapes will appear, and clicking will generate a myriad of different shapes in real time. The shapes can then be stored and used again, either from storage or the Supergraphx toolbar. The shapes in variations are all unique because of the sampling of the parameters over the real numbers. The limited controllability has specific advantages as the user is no longer in full control, but the computer can or will surprise the user. Furthermore, Supergraphx also allows for major savings of time in making shapes in vector-based drawing programs.
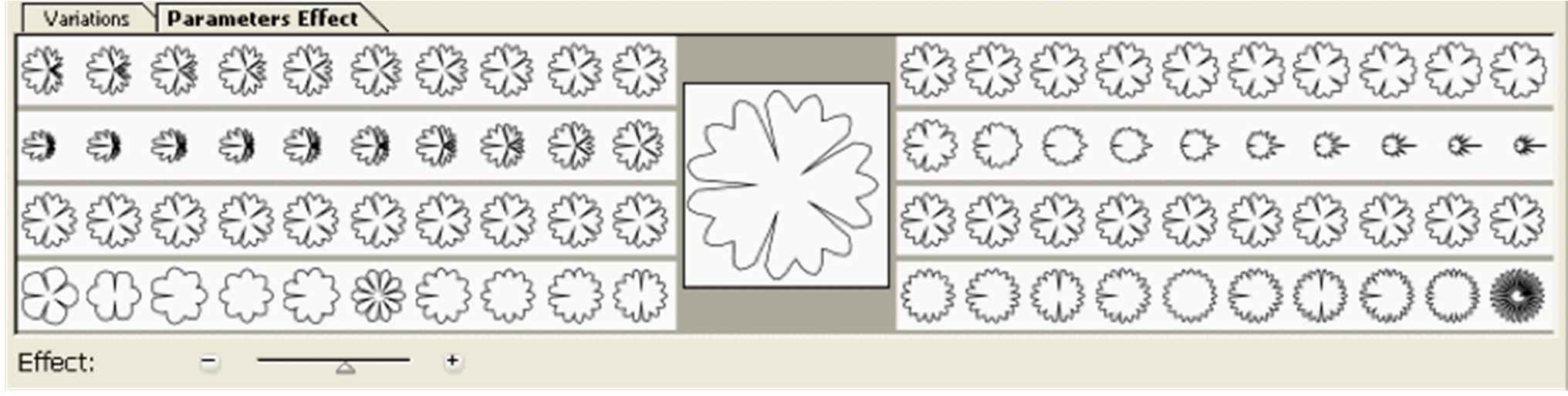
Variations on a shape, as suggested by the software. The user can either choose one of those as the final product or as a starting shape for further exploration.

Supergraphx generates an unlimited variety of unique new shapes based on the Superformula. The shapes above were made in less than 10 minutes.
3.2. Extensions to 3D
Implicit functions based on one single equation can provide different solutions for problems in computer graphics and CAD [23,24]. In this sense, Eq. (4) can be used advantageously for CAD for a unified description of a wide variety of shapes, using a single formula allowing for extremely compact file sizes. There are a variety of ways to extend superellipses and Eq. (4) into 3D, but the selected one is based on the parametric formulation of a sphere, defining two supershapes perpendicular to each other, one as
Eq. (5) can be formulated alternatively as operation

3D supershapes based on Eq. (5).
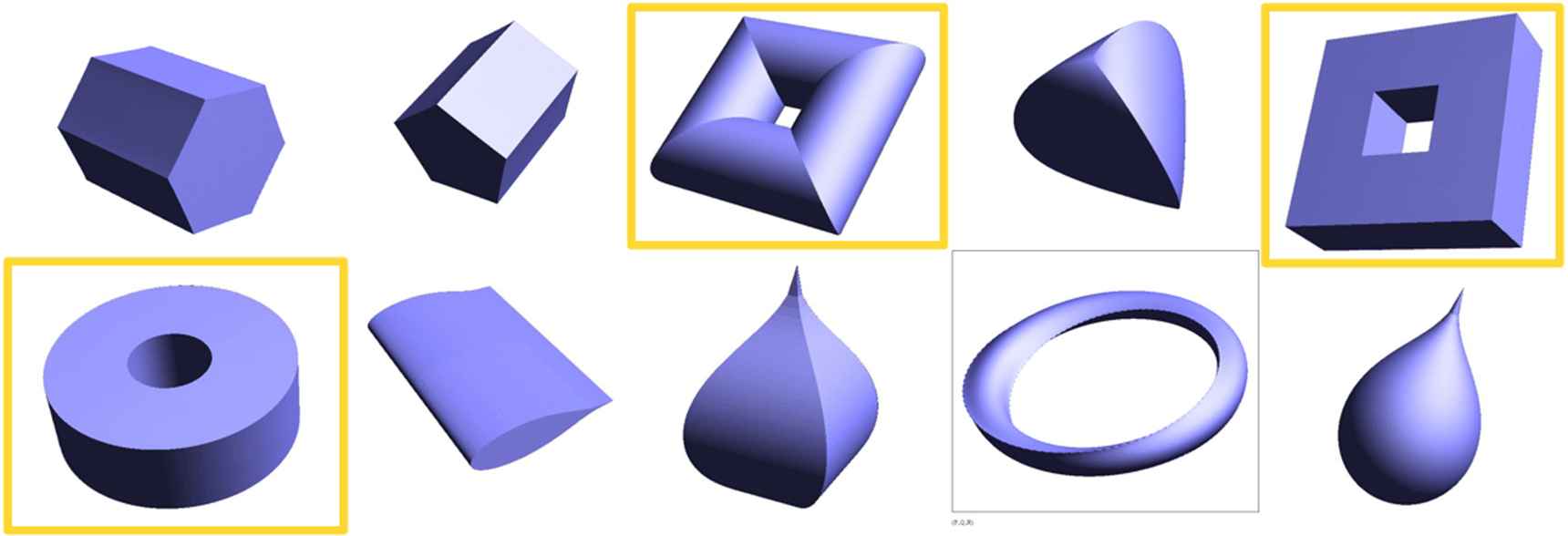
The marked objects had one cross section with an offset from the coordinate system's center line. In the orange boxes, toroidal structures are shown. Bottom row, fourth shape from the left, shows a twisted structure.
This provides a straightforward and intuitive expression for 3D shapes and allows for the development of a simple interface to draw 3D shapes based on two perpendicular sections. In comparison with the sphere, superquadrics and superellipsoids [7,27], various symmetries are possible in different dimensions. In three dimensions non-integer symmetries generate self-intersecting shapes that do not close in one rotation.
Eq. (5) can define a variety of 3D shapes, many of which are well-known primitives, including the well-known extrusions and revolve operations. In addition, knots, helices and spirals can easily be made as well within the same equation. Because of their very nature, not only the outer boundaries of the shapes are defined, but any point on, inside or outside the shape is defined as well (see Fig. 12). A first understanding of the combination of base and height profiles was developed (Fig. 13, Fig. 14) and a Computational Solid Geometry CSG-type modeler was also in an embryonic phase. Development went into higher gear in 2002 and 2003 at Genicap Corporation. Further exploration of the Superformula with multiple symmetries enabled us to massively extend the primitives palette. Along with geometry exploration, numerical calculations and optimization techniques were developed not only for prismatic objects but also for toroidal and helical types of geometry (Fig. 15).
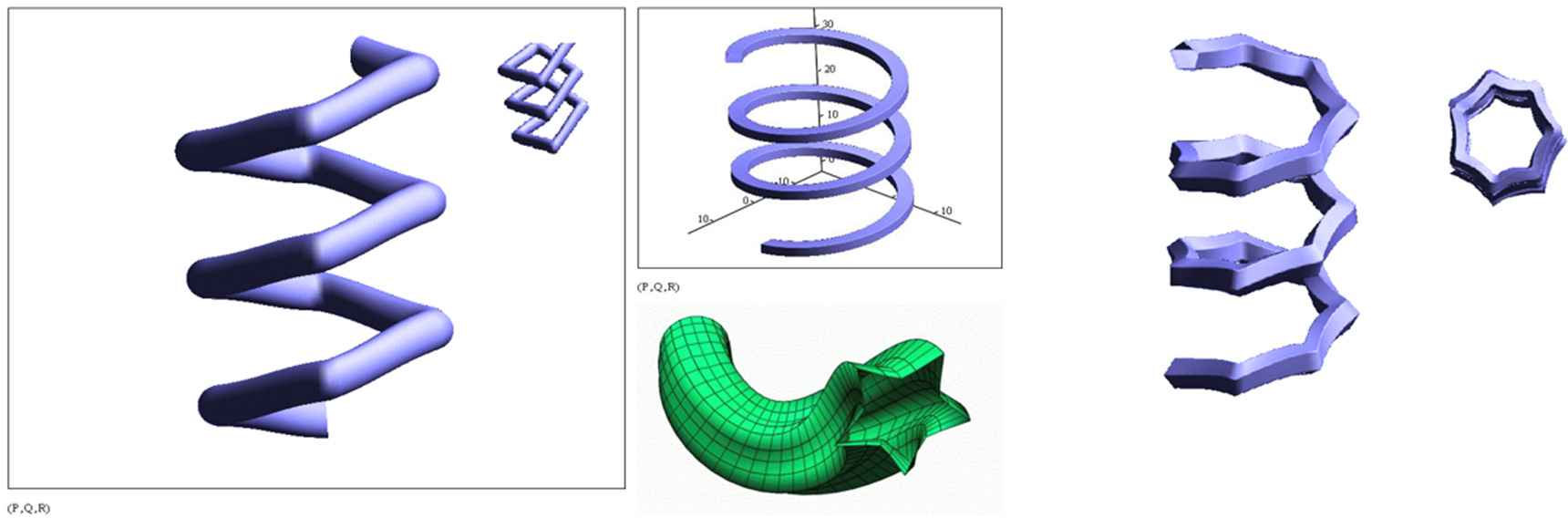
Examples of generalized cylinders and helices. In green, the cross section changes along the path.
By adding a further generalization – a height parameter in function of the base angle was added – the tori were opened up and generalized helices became possible, as extension of generalized cylinders, even enabling morphing from one section type to another over the length of the cylinder’s path (Fig. 15). These developments later merged with the research on Generalized Möbius-Listing surfaces and bodies [28,29].
3.3. 3D Shape Explorer
By changing the parameters of the Superformula, the 3D artist and designer can explore the universe of mathematical objects defined by Superformula equations. The 16 shapes in Fig. 16 left are just a sample from more than 400 interesting shapes made in a 60-minute session using Supergraphx 3D Shape Explorer and a plugin for Cinema 4D. In such a brief session, the artist or designer can generate and evaluate hundreds of different new shapes. The most interesting ones can be selected and stored. A selection can be exported to rendering software for the appropriate texturing and lighting. The computer becomes an extension of human creativity, saving time and moving in entirely new directions to develop a stream of unique shapes. User testimonials of Supergraphx show that “it is like having a brain-storming session with your computer”. Using periodic functions for the path also allows for toroidal structures avoiding self-intersections (Architon, Fig. 16 right) [25,26].

Future Fossils [30] (left) and Architon (right).
3.4. Constructive Solid Geometry and Computer-Aided Design
Furthermore, only extremely small file sizes are needed. Each of these shapes is encoded in less than 40 bytes. Using the shape generator, very complex shapes can be constructed and all shapes can be encoded in less than 20 bytes. The geometric information of all Future Fossils (Fig. 16 left) is stored in 500 bytes only, which is less than the shortcut pointing to that file. Therefore, it is possible to fully encode complex shapes in extremely small files. This Shape Explorer was integrated in a modeler with full parts-assembly structure with definition of Boolean structure. A CSG-type (Constructive Solid Geometry) modeler basically combines shapes using Boolean operations. Classic systems that were on the market at the time were rather primitive and limited to basic shapes which all had to be coded separately. Our approach was to make use of the parametric properties of the Superformula. It was also integrated as a plugin for Cinema 4D and today one finds it also in Blender.
As every shape had the same parameter set, but only changed in shape and size by the value of those parameters, it was understood immediately that the Superformula would be able to define complex geometries with an absolute minimum of data (Fig. 17). A further development was by using R-functions to combine supershapes, allowing to define controllable potential fields on the shapes (Fig. 18) [31,32,33]. R-functions [34] form a natural alliance with superellipses [35,36].

CSG models with file sizes all below 1 kB.
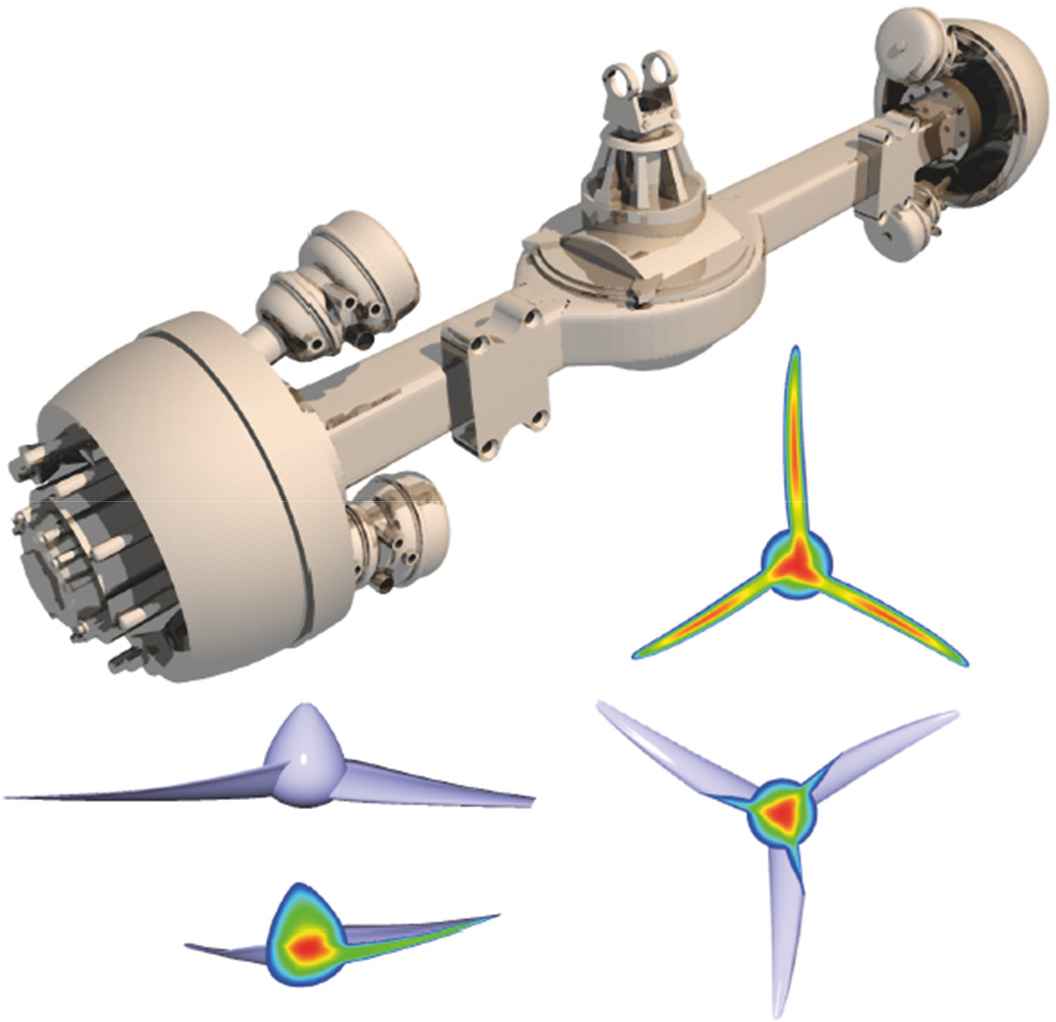
Top: truck axis, consisting of ~250 supershaped parts and ~250 boolean operations. Bottom: view of turbine blades with potential fields [31].
4. OPTIMIZATION
4.1. Formulae for Engineering and Biology
In [10] the polar representation of superellipses was used for computations of area, circumference and inertial moments. After the addition of the symmetry parameter in 1997 (Eq. (4)), focus was set on geometrical exploration and development of tools to compute properties of 2D and 3D shapes. All were based on polar and spherical coordinates.
If we put:
Then the area of a supercircle is:
For the polar moment of inertia
In the same way:
Since the polar moment of inertia is the sum
In the study of square bamboos, which were at the origin of describing natural shapes as superellipses [1,2,37,38], one can easily compute these characteristics for each cross section. Previously, researchers had to resort to specific formulas from engineering, for beams with well-defined cross sections (elliptic, square, circular, T or I beams, ...). Now shapes can be studied with well-defined formulas over a continuous change of cross-sectional geometry along its length and layer thickness. In a study on the structural morphology of petioles of Philodendron melinonii and rhubarb, the shape of the petioles was modeled with Eq. (4) [39,40].
The sections of petioles were scanned and analyzed using the full six parameter set of the Gielis transformations. This was further used to assess the influence of different tissues (parenchyma versus collenchyma) on the torsional stiffness.
The model is also dynamic: the size and shape of cross sections (area and perimeter) of cacti change depending on how much water is stored in the cactus: it will expand after rainfall and shrink in drier periods. Having these characteristics available immediately permits the study of such ratios such as area/perimeter (compactness) or area/polar moment of inertia, etc. In various cases involving multi-objective optimization, superellipses and supershapes (Eq. (2)) are regularly found to be the better solutions, also in technological applications.
4.2. Plant Root Stress Optimization
In [10] the polar form of superellipses was used to generate natural shapes and to perform finite element analysis on these shapes, including the diaphragm of bamboo culms and roots. Many roots in plants have a clear distinction between root cap and root body, whereby the root cap RC consists of stiffer material than the root body. The lower (or distal) part of the root body consists of a quiescent center QC, a primary meristem PM and more proximally the elongation zone where lignification occurs (Fig. 19). Notably, there is a lot of biochemical activity in the quiescent center but cell division, necessary for root growth, occurs on the periphery of this center, not in the quiescent center.
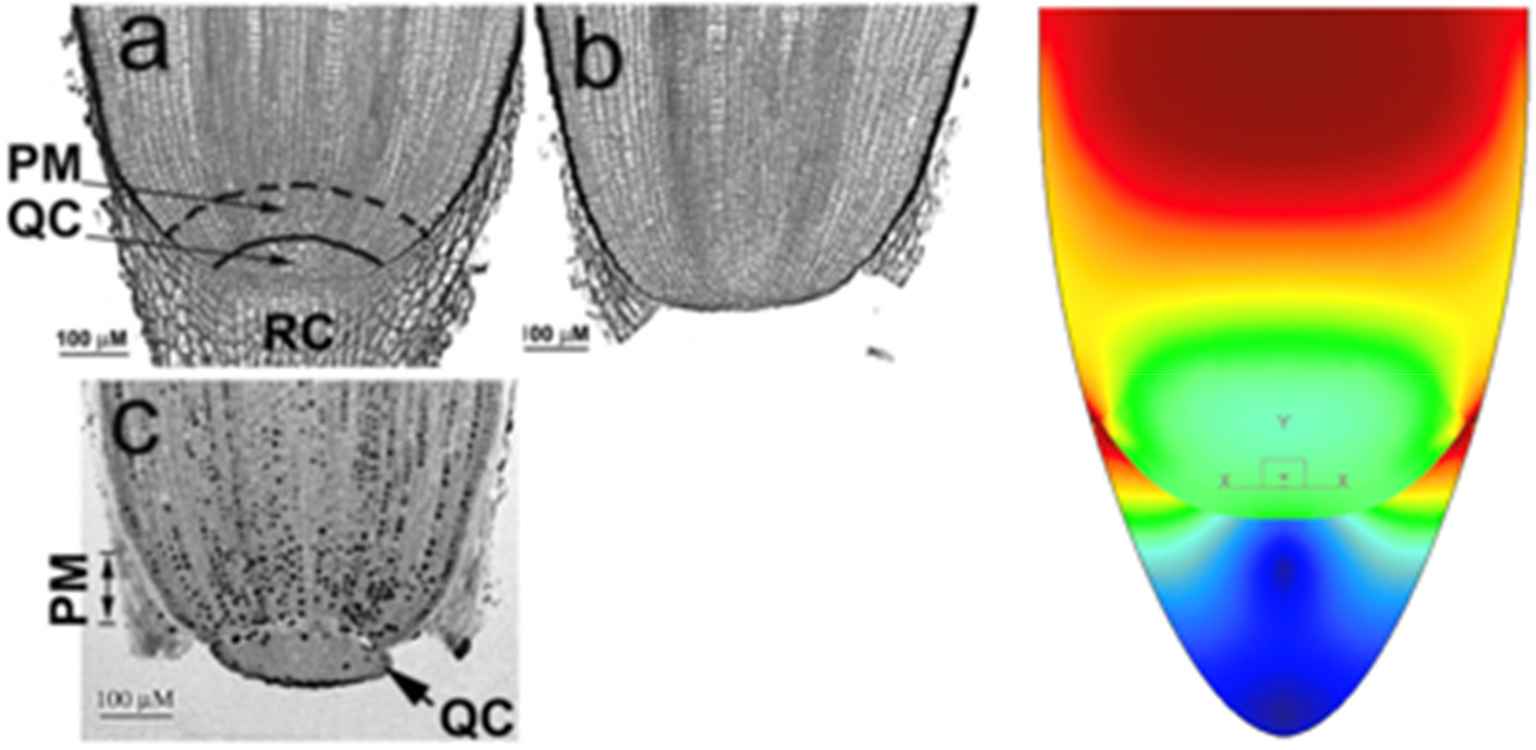
Left: roots of corn, with Flachpunkt-like zone visible in (b); PM is Primary Meristem, QC is Quiescent Center, RC is Root Cap. Right: models with root cap an ellipse and root body a superellipse; the stresses imposed onto the root cap (blue zone) are diverted to the root body (red zone); the central zone (green) remains almost stress-free.
The shape of the root body can be modeled with a superellipse (including a Flachpunkt). Modeling the root body as one half of a superellipse (or as a superparabola) and the root cap as an ellipse, and selecting materials with different stiffness for root cap and root body, is enough to account for the development of a quiescent center (Fig. 19). The force applied at the tip of the root cap results in stress diverted away from the QC and towards the root body, where lignification takes place. The stresses are very low in the quiescent center. However, on the periphery, tension stresses occur which may provide a clue that simple force and shear provide a biomechanical basis for cell division. Applying a stronger force at the tip (axial force) results in a decrease of the quiescent center. A force left or right of the axis, for example when the root tip encounters an obstacle, results in an asymmetrical shape, with more tensile forces at the opposite side of the QC [18]. Once the obstacle is rounded, the gravitropism restores the original growth direction of the root.
4.3. Stress Reduction in Mechanically Stressed Objects
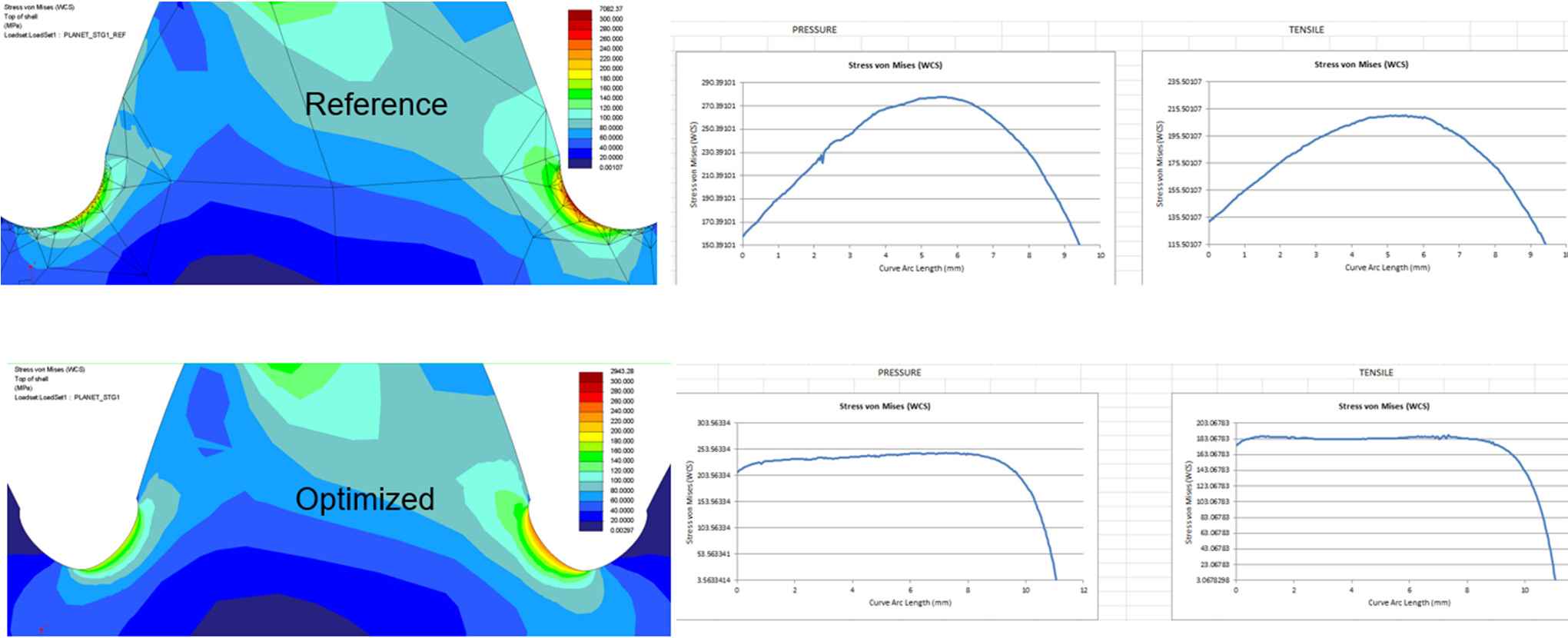
A classical problem in engineering is the study of a plate with circular hole stressed under tension. Without a hole the average tensile stress can be easily calculated as a force over the section surface. With a hole however, local stresses near the hole can increase threefold. This problem can be analyzed easily and accurately using a 2D plane stress FEA (assuming an infinitely thin plate). We were interested in changing the shape of the hole and seeing what shape would yield the lowest stress increase. In the following examples, the plate sections are stressed in Y-direction. The only value being changed in this design is the exponent
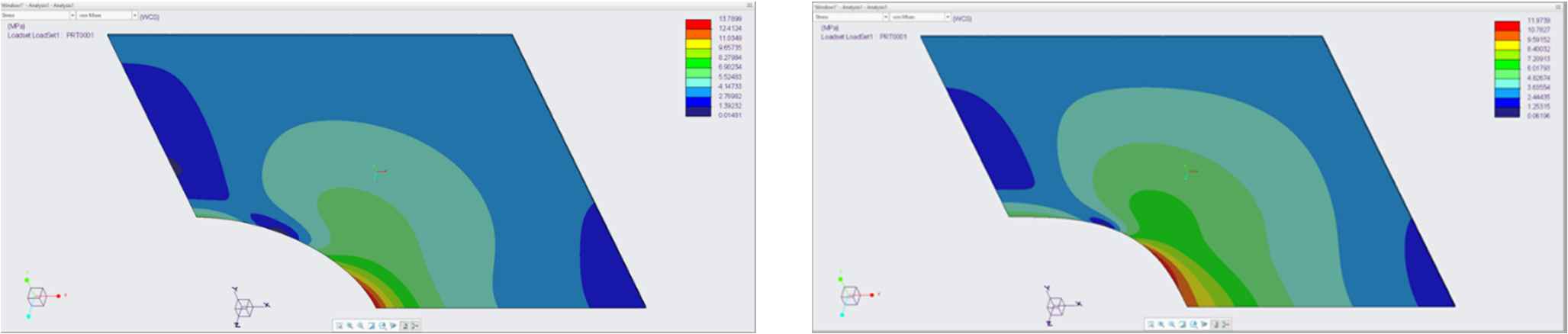
Hole with n = 2 (left) – circular = reference – and n=3.2 (right).
By changing the shape of the hole, the location of maximum stress shifts outside of the horizontal center line of the hole and the maximum stress value reduces. Table 1 lists the maximum occurring stresses in function of the exponent with the minimum stress achieved at n = 3.0.
4.4. Compactness: Dido’s Problem Revisited
Roman poet Publius Vergilius Maro (70–19 BC) tells in his epic Aeneid the story of queen Dido, daughter of the Phoenician king of the 9th century BC. After the assassination of her husband by her brother she fled to a haven near Tunis. There she asked the local leader, Yarb, for as much land as could be enclosed by the hide of a bull. Since the deal seemed modest, he agreed. Dido cut the hide into narrow strips, tied them together, and encircled a large tract of land which became the city of Carthage. Dido intuitively solved what is known as the isoperimetric problem: find among all curves of given length the one curve which encloses maximal area. Unfortunately, most optimization problems feature additional boundary conditions. Dido’s solution was indeed correct, but what if the land she was offered had limitations to shape? Or contained a lot of useless desert? Or a coastline?
At Genicap we worked on compactness, which is a shape parameter that is defined as the ratio between a shape’s area over the circumference. For example, a square with a side of 2 meters has an area of 4 square meters, but a circumference of 8 meters, so its compactness equals 0.5 meters (a length unit). A circle with a radius of 1 meter (= diameter of 2 meters) has an area of
| N | Max. Stress [MPa] | Relative Difference |
|---|---|---|
| 2.0 | 13.7899 | Reference |
| 2.8 | 11.9629 | −13.24% |
| 3.0 | 11.9399 | −13.42% |
| 3.2 | 11.9739 | −13.17% |
Stress in plates with holes.
But could there be a shape available that has an even better compactness than 0.5 meters that is circumscribed by the same square? Intuitively, the expected answer would be positive. But what shape would it be? Defining compactness of a supercircle with exponent n as a ratio:
It results that for a given area of the circumscribed square, a supercircle with
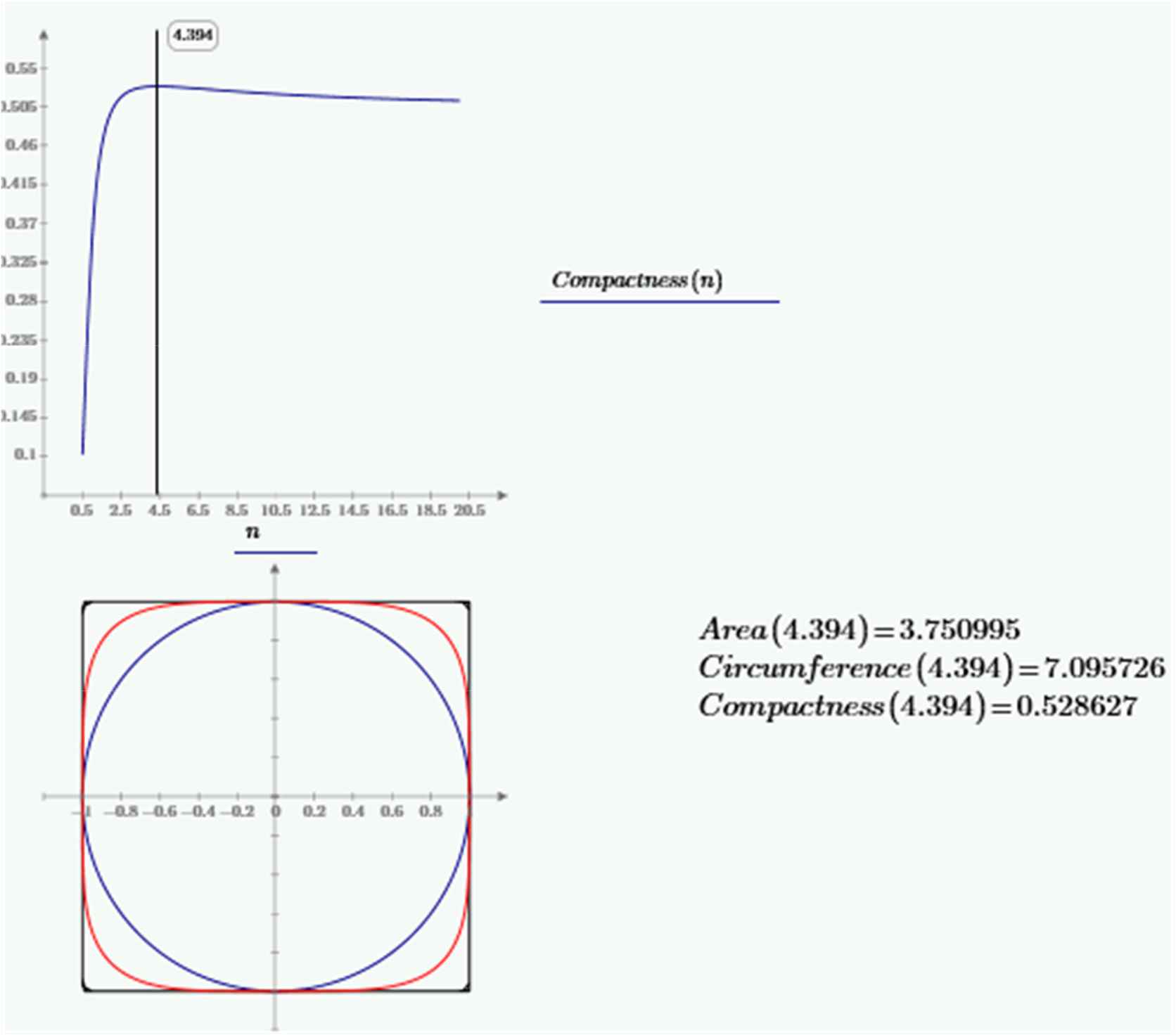
Compactness is calculated in function of the exponent
If a supercircle with
Another, more worldly, problem is the design of a yoghurt pot. In early times, those were cylindrical since these shapes were assumed to be easy to manufacture (by stamping) with the least cost as the shape was thought to be the most compact. Later on, by experience, the pots got more supercircular-shaped to minimize the space between pots. In this problem, space equals money (for storage, transportation, etc.).
A yoghurt pot has a more complex boundary condition as it has to be fastened to other pots at the edge with a given distance between pots, in this case 10mm. By means of adequate modeling and using our numeric calculations, we redesigned the pot and the most optimal design had an exponent of 3.3 (Fig. 22), less than compactness would suggest. By optimizing the shape we were able to reduce the material amount by almost 3% without any loss of functionality. Since these items are produced by millions a day, three percent is a considerable saving. Such optimization can be applied to any optimization in placement, e.g. storage of containers.
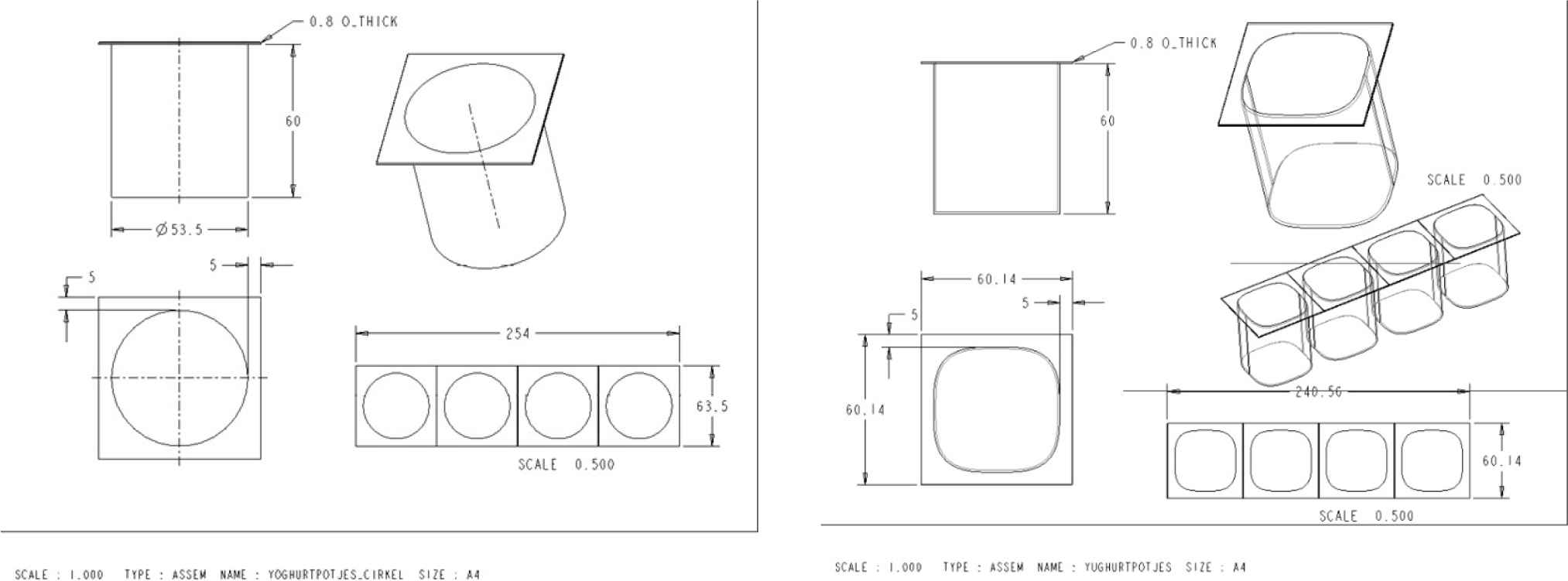
Circular (left) vs. supercircular (right) design of a yoghurt pot.
4.5. Engines and Gears
Another application is in the design of engines. The positioning of valves becomes a lot easier and air inlet of the engine is improved because larger valves can be designed (Fig. 23). Adding to that, the displaced volume is increased for the same size of engine, increasing power output and torque. In today’s engines, injectors spray fuel at a certain inclination and through a limited number of nozzle holes. By applying cylinders with the number of symmetries equal to the number of nozzles, combustion – and thus fuel economy – can be optimized by having a more optimal fuel distribution in the power stroke.
Placement of valves in a superelliptic engine cylinder. A superelliptic cylinder can house much larger valves (green) while maintaining the same distance from the side, improving airflow and combustion properties.
A more complex example is the root design of a gear. The shape of a tooth root is theoretically a trochoid, which is the result of generation using a hob with circular tooth tip profiles. By loading the gear tooth, bending stresses occur in the tooth root, with maximum stresses occurring when the load is applied on a specific spot on the flank (which is depending on the design of the gear and its mating gear). Reducing the root bending stress will have a positive effect on gear life and/or power density of its application. In gear design, by changing the shape of the tooth root by applying a special profile on the generating hob tooth tip, bending stresses can be lowered (Fig. 24).
Changing the tooth root shape can reduce the occurring bending stresses in a gear tooth root.
Also, non-circular gears have been constructed using Eq. (4) [41] and in the design of magnetic gears [42]. Other potential applications could be in roller bearing technology by applying superelliptic microgeometry on the roller elements. The techniques today are already performing well, creating bearings that last a lot longer than in earlier days. But still the question remains whether other profiles could do even better. The application of roller elements shaped as superellipses, the so-called Supereggs by Piet Hein, might produce even better load distributions as the transition from flat surface in the middle to a higher radius on the side of the roller occurs in a smooth and continuous manner. Depending on the occurrence of misalignments, engineers assess whether it is better to focus on one load condition, or to make the roller more robust for misalignments.
5. FUTURE DEVELOPMENTS
Current manufacturing capabilities also allow for more complex mathematical shapes, even with manufacturing technology for nanophotonics and nanotechnology. The above examples show that using superelliptical or superformular shapes are in many ways optimal solutions to complex problems. The author believes that many more optimal designs are possible, once designers and engineers will start to use these insights. There are already many examples in electromagnetics, antenna technology, mechanics, laser optimization, gear technology etc. [3,43,44,45,46]. For antenna technology, the multi-objective optimization method is described by Mescia et al., in this volume, and in [47] the generalized superformula [20] is used to design lens antennas. This is not restricted to single shapes, but also to arrays of shapes, in packaging, antenna arrays and metamaterials [46]. Well established technologies such as gear design and dredge cutter design can greatly benefit from supershape optimization. Such optimization methods also include material minimization via topology optimization [48,49].
One of the most promising applications could be in lasers [45]. In a laser, the laser medium (a gas or a solid) is excited by light or electric power. When the excited electrons fall back to their lower orbitals, they release radiation at a specific frequency. In a laser, a standing wave of this radiation is produced between two mirrors. On one side the mirror is fully reflective, on the other side only partially. As a result, a radiation beam is produced. Both mirrors mostly have circular or flat shapes, thus producing a Gaussian intensity profile.
An idea could be to make the mirrors slightly superelliptical, e.g. with
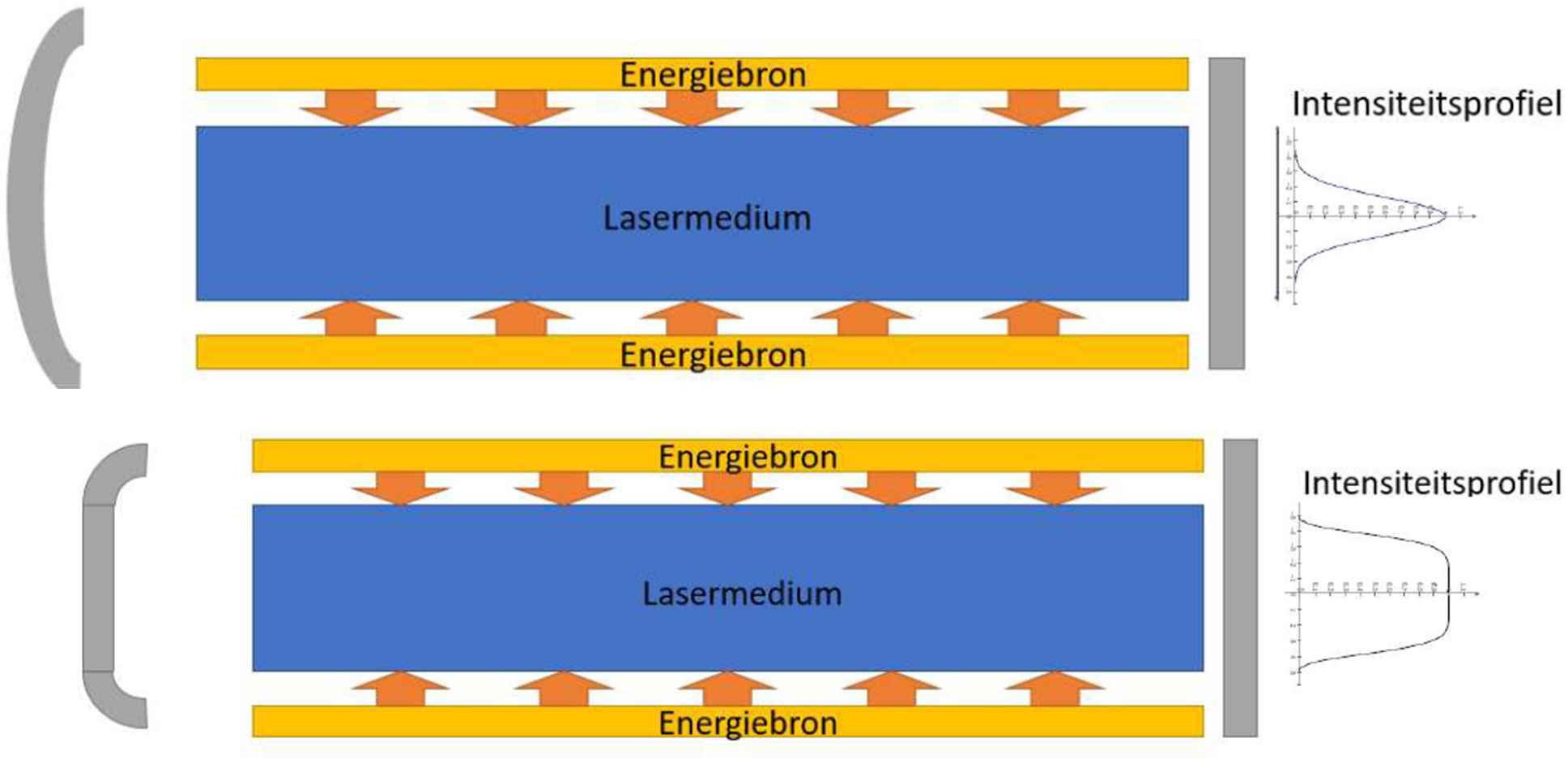
Comparison between a regular laser resonator (top) and a superelliptical resonator (bottom).
REFERENCES
Cite This Article

TY - CONF AU - Bert Beirinckx PY - 2023 DA - 2023/11/29 TI - From Superellipses to Superformula and Technology BT - Proceedings of the 1st International Symposium on Square Bamboos and the Geometree (ISSBG 2022) PB - Athena Publishing SP - 123 EP - 142 SN - 2949-9429 UR - https://doi.org/10.55060/s.atmps.231115.011 DO - https://doi.org/10.55060/s.atmps.231115.011 ID - Beirinckx2023 ER -









