From Pythagoras to Fourier and From Geometry to Nature
DOI: https://doi.org/10.55060/b.p2fg2n.ch011.220215.014
Chapter 11. Stretchable Rulers and Integer Shapes
The geometric sense aids not only in understanding, but also in progress. Andre Weil wrote [105]: “Whatever the truth of the matter, mathematics in our century would not have made such impressive progress without the geometric sense of Elie Cartan, Heinz Hopf, Chern and a very few more. It seems safe to predict that such men will always be needed if mathematics is to go on as before.” Furthermore, understanding historic developments is as important as geometry itself.
11.1 Stretchable Rulers
In Part III it will be shown that the use of a suitable change of coordinates (here referred to as anisotropically stretched polar or spherical coordinates) provides a uniform method to apply the classical Fourier theory even in the case of general normal polar (e.g. starlike) domains. The “exact” solution of many classical boundary value problems in terms of Fourier series can then be achieved, where “exact” means that we can approximate a prescribed finite number of coefficients of the Fourier expansion of the solution as closely as we wish. Hence, the classical Dirichlet, Neumann, Robin problems for the Laplace or Helmholtz equation are always the same, independent of the shape of the domain in which they are considered, provided that this domain can be reduced to a circle (or sphere and cylinder in the 3D case) by a suitable change of coordinates. A prime example of these new coordinates are stretched polar coordinates via Equation (9.23).
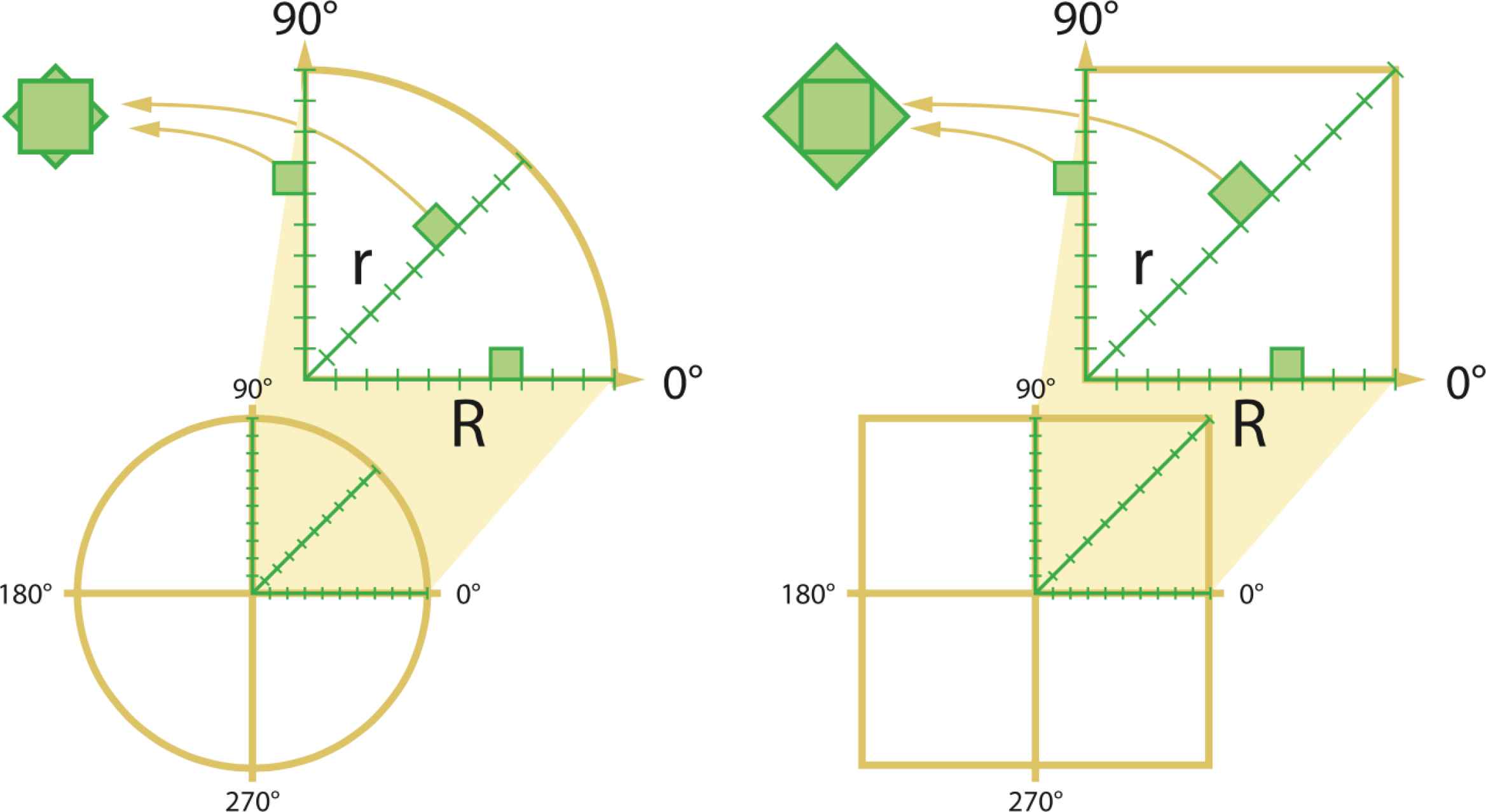
From a geometric point of view however, it is useful to note that this anisotropic stretching is the essence of Gielis Transformations (GT). By using a flexible ruler (the radius vector is shortened or lengthened depending on the angle) GT ensure the commensurability of shapes as diverse as squares, starfish and flowers. But this leads to two different viewpoints: an internal viewpoint (by an observer living inside such a shape) and an external one (looking from the outside with our Euclidean glasses) [41].
If we start with a horizontal vector of length 1, fixed at the center, and we draw a square while keeping the point of the vector on the vertical straight line perpendicular to the horizontal and crossing this axis in the point (1, 0), then our vector will stretch to
Using a stretchable ruler to draw a square, but it is a unit circle anyway [41].
Instead of an elastic ruler we imagine that to the origin we attach various springs in different directions. These springs all have the same length and same spring characteristics. If we stretch them, two conditions may occur. We can stretch them with equal force or we can stretch them to a certain fixed distance. Say we stretch the spring by 1 cm. In both cases, all end points of all stretched springs will define a circle. The fact that we can consider both force and distance is given by the simple relation
Now let us try to draw a square with our springs. In the traditional view, if we want to draw a square, at 0° we do not stretch the spring and take this as distance 1. To draw the point at 45° the spring is stretched by a factor of
11.2 Shapes as Integers
Fourier series and generalized Fourier series can be thought of as numbers with, respectively, circle and Lamé-Gielis curves as “integers”. In Figure 28, the outline of a bird is shown which is built up from three curves. The notation k = 3 refers to the number of shapes added together, but is inspired by the theory of k-type curves. The k-finite type curves were defined in the framework of submanifold theory [28]: curves are of infinite or finite type depending on whether their Fourier expansion with respect to arc length is infinite or finite. One consequence of the theory of k-type curves is that the circle is the only closed planar curve that is of finite type, namely of 1-type (1-T) with all cosine and sine terms equal to zero. Any other curve necessarily has an infinite Fourier expansion and is of infinite type (∞-T).
Series expansions, like Fourier, can be considered as a positional system with an integer part a0 and a “decimal part”. 1-type curves are “integers”, while (∞-T) curves are “irrational” numbers since they have no recurring sequences. Note that the inspiration for the development of infinite series by Newton came from the decimal system developed one century earlier by Simon Stevin. Instead of using numbers, Newton introduced functions [50]. According to the k-type curve theory there is only one shape which is an integer, namely the circle. All other shapes have an infinite Fourier series expansion, i.e. an infinite “decimal” part. An alternative interpretation is that all curves other than the circle, including the ellipses, are equally complex: once their Fourier expansion starts, it never stops [103]. Their expansion contains infinitely many terms (∞-T). It is quite remarkable that a system based on the transcendental number π, or in the case of transforms on the base of the natural logarithm e (another transcendental number), generates only one “integer shape” (the circle of radius R = a0), whereas all other shapes have an infinite “decimal part”.
In contrast, using Equation (10.8), any curve with a stretchable radius a0ρ0 defined by Equations (9.5a) and (9.5b) or Equation (9.23), is of 1-type and their expansions, once they start, stop immediately since all cosine and sine terms are zero. Hence, all Lamé-Gielis curves in this sense need no further expansion and can thus be regarded as an “integer”, albeit an integer defined intrinsically by an n-tuple of parameters. The value of n is somewhere between 5 for superellipses (Equation 9.5b; Section 9.2) and 7 (Equation 9.23). Lamé curves and superellipses constitute a 4- or 5-dimensional manifold (see Section 9.1). Hence all these “integer” shapes are points of a sufficiently low-dimensional manifold. Consequently all Gielis curves, including the circle, ellipses and Lamé curves, are equally simple in this generalized Fourier sense, in addition to the Pythagorean compact and topologically simple nature of the equations. With each integer-shape a specific πn and dedicated trigonometric functions are associated, but Gielis transformations provide for a one-to-one key between all.







