From Pythagoras to Fourier and From Geometry to Nature
DOI: https://doi.org/10.55060/b.p2fg2n.ch014.220215.017
Chapter 14. Understanding Life
14.1 Commensurability and Computability
In the past decade, over 40,000 biological specimens have been tested. In starfish, plant leaves, seeds and tree rings there are excellent agreements between model and real measured data, but in both cases two parameters for superellipses suffice. Circles and ellipses, the ideal shapes from Euclidean geometry, are rarely observed, also not in tree rings. They are not deviations of the circle, or near-circles, but their shape is superelliptic. Richard Feynman wrote: “We have in our minds a tendency to accept symmetry as some kind of perfection. In fact, it is the old idea of the Greeks that circles were perfect, and it was rather horrible to believe that the planetary orbits were not circles, but only nearly circles. The difference between being a circle and being a nearly-circle is not a small difference. It is a fundamental change so far as the mind is concerned. There is a sign of perfection and symmetry in a circle that is not there the moment the circle is slightly off. That is the end of it, it is no longer symmetrical. Then the question is why it is only nearly a circle – that is a more difficult question.” [34]
What we find in biology are not small deviations from the ideal circle, nor are they nearly circles, in which symmetry vanishes. On the contrary: they are genuine supercircles and superellipses (or subcircles and subellipses) with their own internal (and perfect) symmetry. The absence of circles and ellipses in biology challenges the validity of physics methods based on the classical Pythagorean theorem and on conic sections in applications in biology.
A fundamental question in the natural sciences has always been about measurements and metric geometry: “how to measure, with what yardstick?” A search for a common measure or yardstick has always been essential and symmetry has the very same origin. Symmetry (-metria) for the Ancient Greek mathematicians meant proportion or right balance and the verb “to symmetrize” is the deliberate act of making objects commensurable, forming the real basis of mathematics and geometry. Gielis transformations, which are essentially a generalization of the Pythagorean theorem and of conic sections, allow for a uniform description of a wide range of abstract and natural shapes. This opens the door for a geometrical theory of morphogenesis, which is similar to a geometrization of nature (not only of physics). In a geometric way, Gielis curves make natural shapes, objects and phenomena commensurable (i.e. symmetric). In Chapter 13 a range of shapes is shown that are created with Equations (9.23) and (9.24) or the 3D versions thereof.
Beyond the descriptive and the computational, natural shapes and phenomena are subject to external and internal forces. The best examples are soap films and soap bubbles, which are examples of stress minimization on their surfaces. Such stresses are also referred to as natural curvature conditions. Natural curvature conditions are the reason why soap films and soap bubbles are optimal solutions to given problems: that of arranging a soap film, minimizing stress on its surface while balancing the pressure inside and outside of the soap bubble.
14.2 Constant Anisotropic Mean Curvature Surfaces
The nearly universal principle in the natural sciences is that the equilibrium configuration of a system can be found by minimizing its total energy among all admissible configurations. When we are considering the surface interface between two or more immiscible materials, the surface geometry is determined by minimizing the surface tension subject to whatever additional constraints are imposed by the environment. These constraints may take the form of boundary conditions or may include constraints that the volume or even the surface area be preserved under deformations. In addition, there may be additional energy contributions depending on the boundary. There may also be energy contributions arising from external forces such as gravity. For materials, which are in an ordered phase, the interfacial energy may be anisotropic, i.e. its density may depend on the direction of the surface. This is particularly true of the surface of a crystal, a fact that is empirically obvious from the way that the surface geometry tends to favor certain directions.
There is a canonical equilibrium surface, called the Wulff shape, that can be characterized as the absolute minimizer of the free energy F among all surfaces enclosing the same three-dimensional volume as the Wulff shape [63, 64]. Other natural curvature conditions are for example the Willmore conditions with the Willmore functional ∫ H2dA, the integral of the squared mean curvature over the total surface, which has been used to study membranes.
This is the governing principle of why soap films, snowflakes, cells and membranes, flowers and space-times have the shape they have. As surfaces residing in a 3D world, all flowers and plants conform to the geometrical and mathematical principles of surface theory. This includes inequalities between means of principal curvatures on a surface k1, k2 to describe stress in a point. These principal curvatures are the maximal and minimal curvatures and they are perpendicular! In geometry one compares the arithmetic mean AM and the geometric mean GM of the two principal curvatures. Furthermore, in the same way as describing shapes as Lamé curves, relations between classical principal curvatures can also be superelliptic with the Casorati curvature for n = 2 (Figure 58).
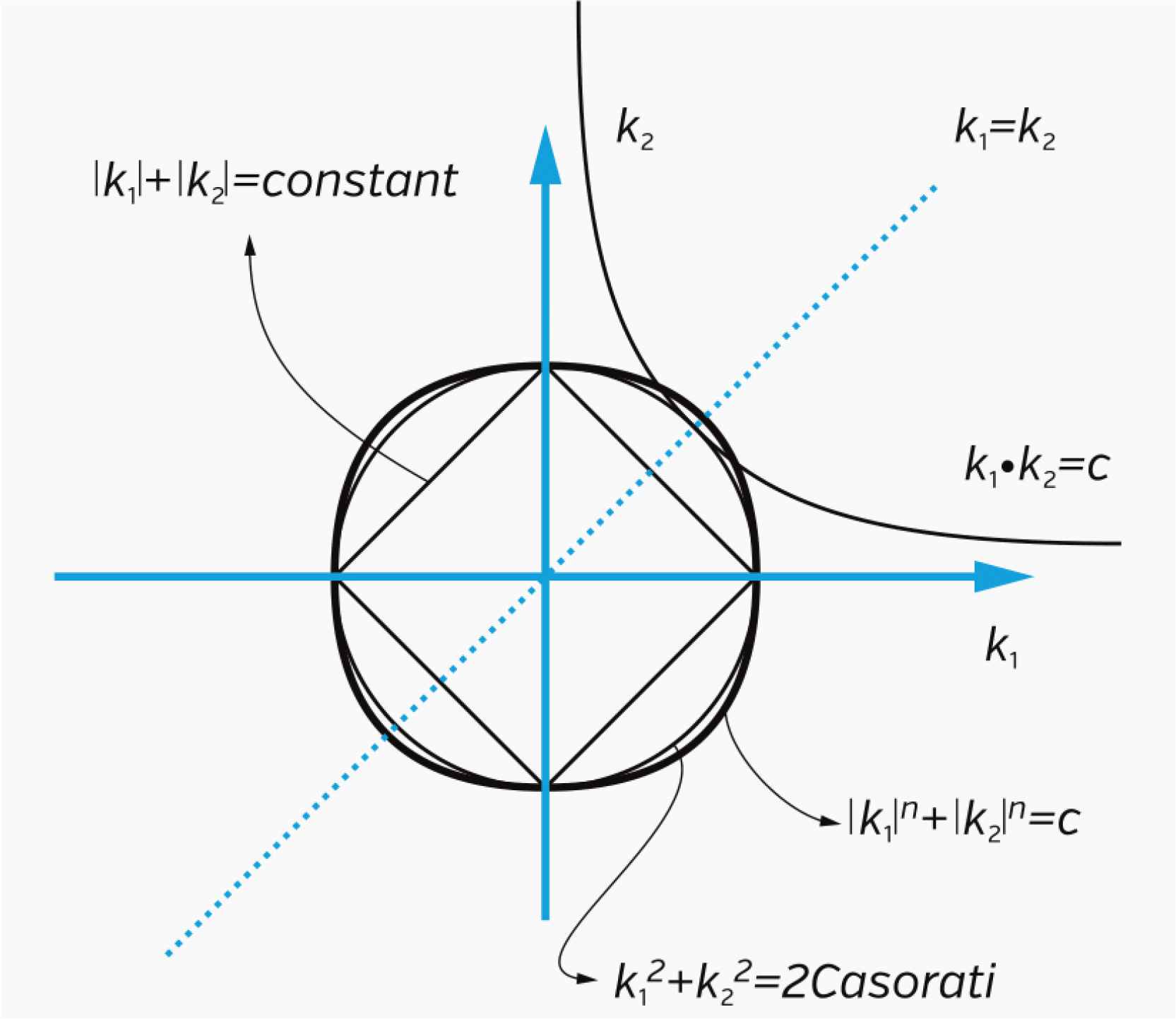
Possible configurations between principal curvatures in a point P on a surface [41].
For soap bubbles and films, the Gaussian curvature K = k1 ⋅ k2 (a quantitative measure of stress on the surface; the square of the GM) and mean curvature
These classical CMC surfaces have been extended to the anisotropic case, to Constant Anisotropic Mean Curvature surfaces with GT, whereby the surface energy is distributed along a prism (rather than spherical as for CMC) [63]. The result is a ‘supershaped’ catenoid (Figure 59) which is found in natural snowflakes. Cushion starfish of the genus Culcita (Figure 60) are an example of the experiments that nature has run, developing shapes intermediate between the archetypical shape of starfish (e.g. Anthenoides and Stellaster in Figure 45) and soap bubbles. In fluid mechanics other examples of supershapes are known (Figure 61; [42]).

Left: prism and supercatenoid. Center: prismatic snowflakes. Right: capped column snowflakes.

Cushion starfish [41].
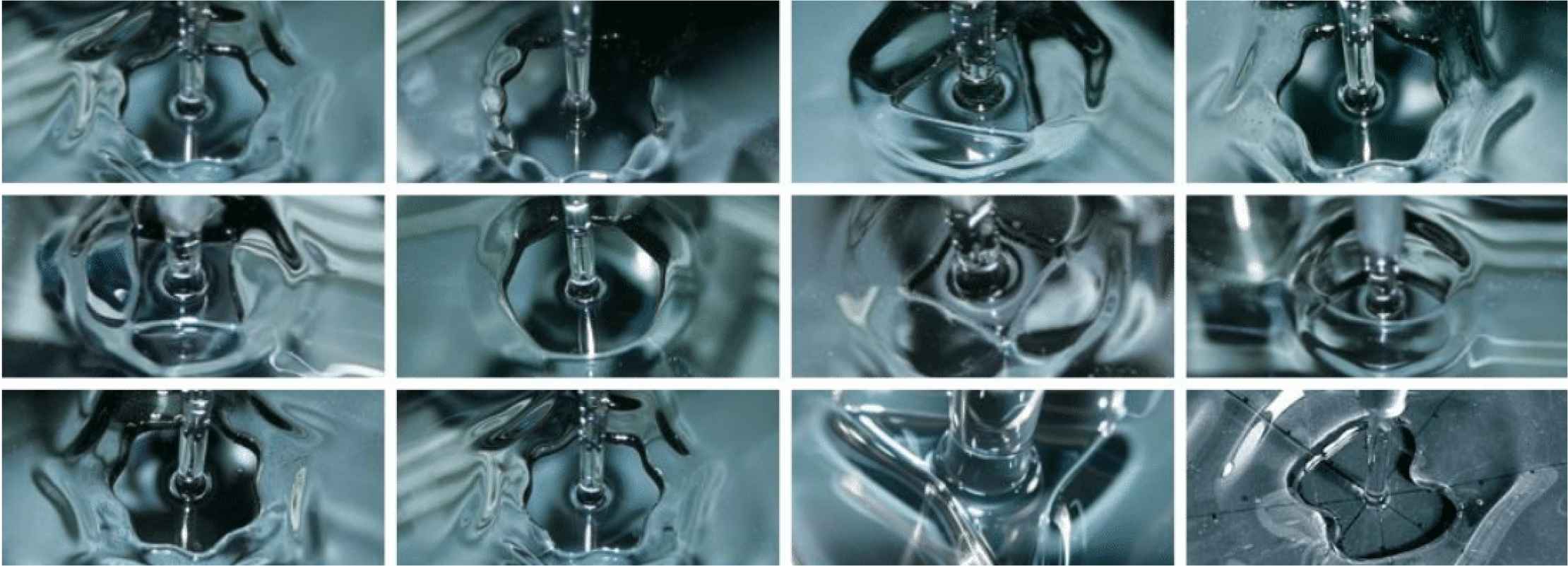
Supershape patterns in viscous fluids [42].
In one stroke our knowledge is extended from minimal surfaces in soap films to real surfaces and bodies in the natural sciences, and this is valid from the hyperlarge to the ultra-small. The curved surfaces we observe everywhere can be studied as solutions to (multi-objective) optimization problems. Growth and development are about getting rid of stress induced by the environment, both external (e.g. light, heat, humidity, nutrients) and internal (e.g. turgor pressure). This is what the Laplace equation is about.
Instead of avoiding curvatures and tending towards equilibrium shapes, in nature a “stabilization” of curvature in solid shapes seems to be quite a general rule, integrating curvature in the most direct way. Sand dollars are one example. In Figure 62 on the right, a pentagonal supershape is shown with its curvature in blue. In the center, the flower-like openings in the shell of a sand dollar can be seen. These provide opportunities for food collection since the tube feet extrude from these flower-like openings. The curvature comes naturally with the slightest deviation from a circle into a supershape. In a sand dollar, curvatures are functionalized by the test of the sand dollar and through the openings the tube feet can function.
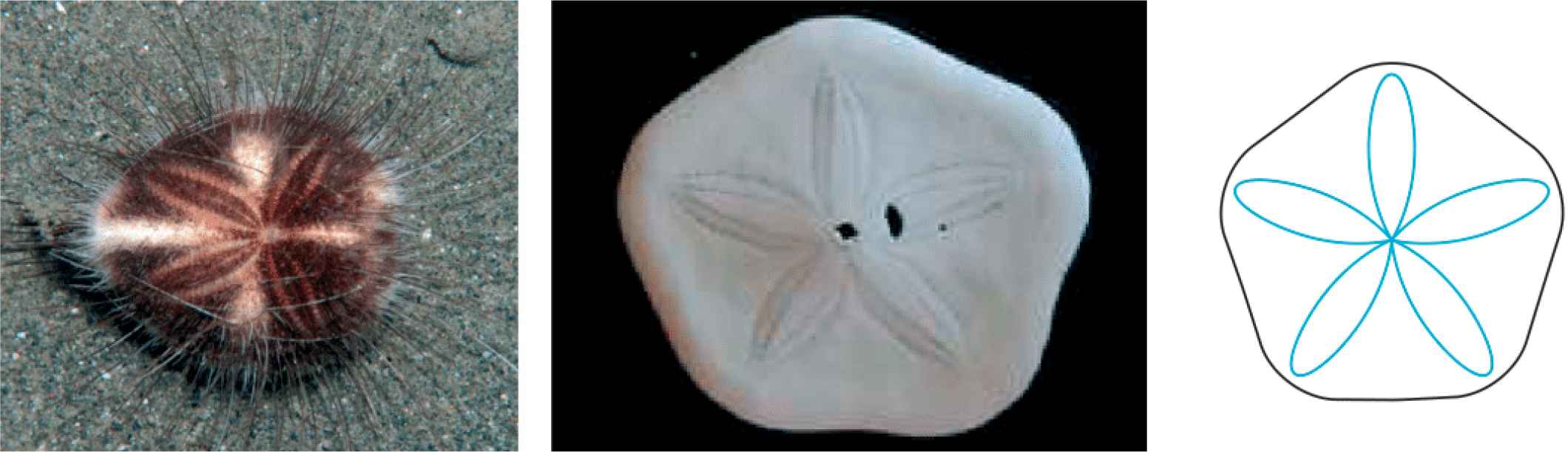
Left: Maretia planulata (sand dollar). Center: flower-like openings in the shell of a sand dollar. Right: pentagonal supershape in black with its curvature in blue (m = 5; n1 = 5; n2,3 = 3.2; A = B = 1.7).
14.3 Natural Shapes from a Geometrical Vantage Point
Natural shapes can be considered as two opposite reactions to tension induced by the environment. When the tension in the shape aligns with the growth vector, the resulting shape is the circle. When the shape growth completely opposes the tension, the resulting shape is the logarithmic spiral [56]. These are the two basic shapes in nature, from a purely geometrical viewpoint. By applying Gielis transformations (GT) to these two basic shapes, a very wide range of natural shapes can be studied in a simple way: take one of the two basic shapes and extract the anisotropy (or curvature) via GT (Figure 63). That is, the function:

GT on a circle and logarithmic spiral.
In Figure 64, examples of the transformation of logarithmic spirals (the polar representation of the exponential function) are shown. The quintessential example of logarithmic spirals in nature are Nautilus shells (Figure 64 bottom right). Here the value of GT is equal to one. Such “continuous” growth (i.e. the spiral without transformations) is also observed in snails (Figure 64 right bottom row). Most mollusk shells however display an anisotropic growth.

Left: Soliclymenia paradoxa fossil. Bottom right: Nautilus pompilius L.
14.4 Curvature Can Be Based on the Shape Itself
The first to understand in detail that rulers could be stretchable and at the same time have a precise quantitative meaning, were Einstein and Poincaré: they understood that measured data could be interpreted in a new framework of Special Relativity Theory (SRT) in which time or mass lose their absolute meaning. All becomes relative, depending on who measures and interprets. It is no miracle then that Gielis transformations are a more general form and the Lorentz-Fitzgerald transformations of SRT are a special case. The intrinsic or extrinsic view depends on the observer: living in the space or looking from the outside (Chapter 11; [41]). Another example is General Relativity Theory (GRT), namely space-time metrics of the Big Bang type which are formal deformations of Pythagoras’ theorem, similar to the deformations of Euclidean circles or spheres with Gielis transformations, whereby the space-slices of the full space-time at any given time t are Riemannian 3D-spaces of constant curvature c(t) [47]:
The notion of the notion of curvature can then also be generalized. In the Oresme-Newton tradition, the dominant view in science, curvature of curves is compared with the classic Euclidean circle. It is a pointwise procedure and the radius of this circle is called the radius of curvature. Consequently, one curve has a circle of curvature which is the curve itself and that is the circle. In all other cases the procedure becomes pointwise, i.e. in each point of a curve we need to determine the best fitting circle.
The alternative is to start from the unit circle and use this as an osculating curve. Then any normal polar shape can be used and the process is global too, not local. Fitting is then no longer a local process of fitting a circle to a point on a curve, but it becomes a global process for the complete shape, much in the same way as the osculating circle fits a circle everywhere (Figure 65). Hence this process of defining curvature is global rather than local (or “glocal” as referring to a zone rather than to a point).

Left: the classic result of rotating a red circle relative to a green one. Center and right: a chain is rotated along the curve following the space.
Starting from this novel type of shape description and curvature of shapes, we can define, analogous to curvature of curves using circles, Lamé curvatures kL (14.2) and Gielis curvatures kGT (14.3):
Science’s current main tools are based on the circle as the osculating curve, which is also the basis for the calculus. In a like manner, we can use Lamé-Gielis curves as osculating curves and derive calculus from thereon. A further step is then the generalization for the anisotropic case of Newton’s law of gravitation and Coulomb’s law for electrostatic attraction, both depending on the square of the distance between two masses or two masses or charges, namely 1/ρ2(ϑ).
14.5 New Lenses for 20/20 Vision in the Natural Sciences
We build models about our observations of natural phenomena and shapes. Observations in botany led to the generalization of Lamé curves to Gielis transformations and to the notion of Universal Natural Shapes, where one generalization of the Pythagorean theorem leads to a unified description of natural shapes, great and small, living and non-living. For our observations, perception is crucial. In the early days after discovering Lamé curves to model plants and flowers, several botanists and others replied that the shapes of Marsilea leaves or Hydrangea sepals (Figure 66) are round or circular. The same answer from artists or scientists. But when they were shown Lamé curves they all immediately agreed that these shapes were indeed Lamé curves, intermediate between circle and square.

Left: leaves of Marsilea. Center: sepals of Hydrangea “Blue Wave”. Right: a snowflake with short and long sides.
Ice has a molecular symmetry of six and most well-known snowflakes indeed have this hexagonal symmetry. In Figure 66, a snowflake is shown with alternating long and short sides. The general view is that it is a truncated triangle. A classical Fourier series would indicate a strong amplitude at 3. Some form of symmetry-breaking or reduction has occurred and the original hexagonal symmetry of ice is reduced to three. However, if we look through our new glasses, the result with Equation (9.23) is that we see a hexagon with short S and long L sides. Just as a rectangle with S-L-S-L sides is obtained from a square with all sides equal by stretching in one direction, now for the hexagon we have S-L-S-L-S-L. But despite this change, it remains a hexagon with its symmetry of six and all snowflakes retain the original symmetry of ice.
The key is that Lamé-Gielis transformations provide for new glasses and lenses to study nature, in which many different fields of science can be unified. By generalizing Lamé’s work (200 years ago) we arrived at a 21st-century version of the Pythagorean theorem (2,500 years ago). With our new glasses we see more structure than chaos, more redundancy than entropy and continuous transformations between shapes. Circles and squares, ellipses and polygons, starfish and flowers, are no longer different, but one family of geometrical shapes. It allows for a quantification of the qualitative in nature. With these lenses we can study natural shapes from the point of view of curvature and natural shapes as transformations of circle and spiral in the 2D case. Gielis transformations are an effective geometric approach to deal with some of the global anisotropies in many forms that do occur in nature and with imperfections or certain kinds of repeated local deviations from Euclidean perfection in such forms.
Gielis transformations have found hundreds of applications in technology ranging from antennas to lasers, from data processing to nanotechnology, from virtual reality to sounds, and more (see [39]). Figures 67 and 68 left and center show a collection of shapes that differ from sphere and torus in a few parameters only. Figure 68 right shows gold nanoparticles, whereby the shape can be adjusted to improve heat distribution in cancer research.

A collection of shapes that differ from sphere and torus in a few parameters only.
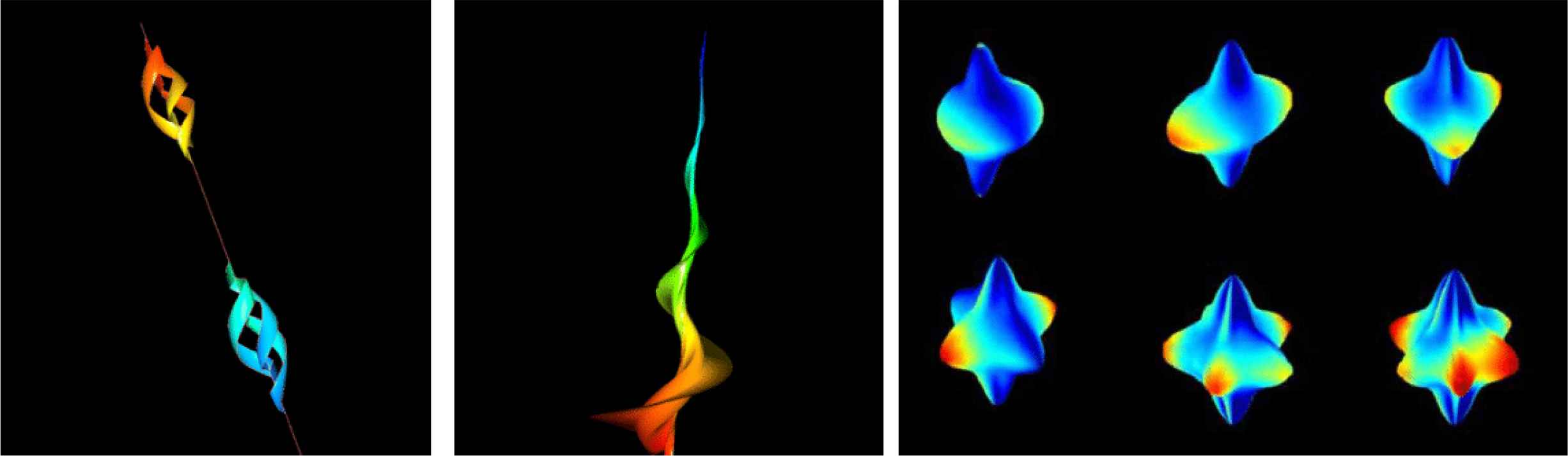
Left and center: wave packets and turbulent movements. Right: gold supershaped nanoparticles [85].
A continuous transformation in just a few parameters (a low-dimensional manifold) opens doors for all technologies [39]. The main advantages include:
Ultra-compact representations of shape and change: only a few numbers suffice (Figure 67);
Uniform description, also for combinations of shapes [36];
A continuous transformation between shapes (kinematics and dynamics);
Multi-objective optimization using only a few parameters [4];
Ultra-fast computations of solutions [54].







